
分析 由题意可得m,n为ex+a=2x的两个不等实根,根据导数的几何意义求出切线方程,即可判断a的范围
解答  解:f(x)=ex+a在∈[m,n]上为增函数,
解:f(x)=ex+a在∈[m,n]上为增函数,
∴f(x)∈[em+a,en+a],
∵函数f(x)=ex+a,x∈[m,n]的值域为[2m,2n],
∴$\left\{\begin{array}{l}{{e}^{m}+a=2m}\\{{e}^{n}+a=2n}\end{array}\right.$,
∴m,n为ex+a=2x的两个不等实根,
即y=ex,y=2x-a有两个不同的交点,
设切点为(x0,y0),
∵y′=ex,
∴e${\;}^{{x}_{0}}$=2
∴x0=ln2,
∴y0=2,
∴-a>2-2ln2,
即a<-2+2ln2,
故答案为:(-∞,-2+2ln2).
点评 本题考查了函数的值域和函数的单调性以及函数零点的问题,属于中档题


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
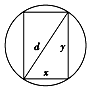 如图,横梁的横断面是一个矩形,而横梁的强度和它的矩形横断面的宽与高的平方的乘积成正比,要将直径为d的圆木锯成强度最大的横梁,则横断面的高和宽分别为( )
如图,横梁的横断面是一个矩形,而横梁的强度和它的矩形横断面的宽与高的平方的乘积成正比,要将直径为d的圆木锯成强度最大的横梁,则横断面的高和宽分别为( )| A. | $\sqrt{3}$d,$\frac{\sqrt{3}}{3}$d | B. | $\frac{\sqrt{3}}{3}$d,$\frac{\sqrt{6}}{3}$d | C. | $\frac{\sqrt{6}}{3}$d,$\frac{\sqrt{3}}{3}$d | D. | $\frac{\sqrt{6}}{3}$d,$\sqrt{3}$d |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=2cos2x | B. | y=2sin2x | C. | y=1+sin(2x+$\frac{π}{4}$) | D. | y=cos2x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈(0,π),sinx=tanx | |
| B. | 条件p:$\left\{\begin{array}{l}{x+y>4}\\{xy>4}\end{array}\right.$,条件q:$\left\{\begin{array}{l}{x>2}\\{y>2}\end{array}\right.$,则p是q的必要不充分条件 | |
| C. | “?x∈R,x2+x+1>0”的否定是“?x0∈R,x02+x0+1<0” | |
| D. | ?θ∈R,函数f(x)=sin(2x+θ)都不是偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 130 | B. | 65 | C. | 70 | D. | 140 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{5}{6}$ | C. | -$\frac{3}{4}$ | D. | $\frac{6}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com