
分析 (1)由题意可得:共有2$({∁}_{2}^{2}{∁}_{2}^{1}•{∁}_{1}^{1}+{∁}_{2}^{2}{∁}_{2}^{2}{∁}_{1}^{1})$种不同的分配方案.
(2)对于两个公园分配人数分别为:0,5;1,4;2,3;3,2;4,1;5,0.可得ξ=|X-Y|的取值分别为:1,3,5.于是P(ξ=1)=$\frac{2{∁}_{5}^{2}{∁}_{3}^{3}}{{2}^{5}}$,P(ξ=3)=$\frac{2{∁}_{5}^{1}{∁}_{4}^{4}}{{2}^{5}}$,P(ξ=5)=$\frac{2{∁}_{5}^{5}}{{2}^{5}}$.
解答 解:(1)学生甲和乙必须在同一个公园,且甲和丙不能在同一个公园,则共有2$({∁}_{2}^{2}{∁}_{2}^{1}•{∁}_{1}^{1}+{∁}_{2}^{2}{∁}_{2}^{2}{∁}_{1}^{1})$=6种不同的分配方案.
(2)对于两个公园分配人数分别为:0,5;1,4;2,3;3,2;4,1;5,0.
∴ξ=|X-Y|的取值分别为:1,3,5.
∴P(ξ=1)=$\frac{2{∁}_{5}^{2}{∁}_{3}^{3}}{{2}^{5}}$=$\frac{20}{32}$=$\frac{5}{8}$,P(ξ=3)=$\frac{2{∁}_{5}^{1}{∁}_{4}^{4}}{{2}^{5}}$=$\frac{10}{32}$=$\frac{5}{16}$,P(ξ=5)=$\frac{2{∁}_{5}^{5}}{{2}^{5}}$=$\frac{2}{32}$=$\frac{1}{16}$.
可得ξ分布列:
| ξ | 1 | 3 | 5 |
| P | $\frac{5}{8}$ | $\frac{5}{16}$ | $\frac{1}{16}$ |
点评 本题考查了随机变量的分布列及其数学期望、组合数的计算公式、分类讨论方法、古典概率计算公式,考查了推理能力与计算能力,属于中档题.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | -20 | C. | $20\sqrt{3}$ | D. | $-20\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
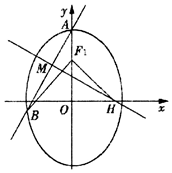 已知椭圆C:$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1({a>b>0})$的上、下焦点分别为F1,F2,上焦点F1到直线 4x+3y+12=0的距离为3,椭圆C的离心率e=$\frac{1}{2}$.
已知椭圆C:$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1({a>b>0})$的上、下焦点分别为F1,F2,上焦点F1到直线 4x+3y+12=0的距离为3,椭圆C的离心率e=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
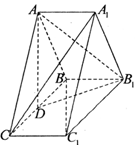 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,D为棱BC的中点,AB=AC,BC=$\sqrt{2}A{A_1}$,求证:
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,D为棱BC的中点,AB=AC,BC=$\sqrt{2}A{A_1}$,求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com