
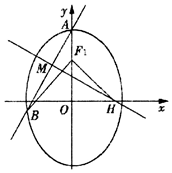
 已知椭圆C:$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1({a>b>0})$的上、下焦点分别为F1,F2,上焦点F1到直线 4x+3y+12=0的距离为3,椭圆C的离心率e=$\frac{1}{2}$.
已知椭圆C:$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1({a>b>0})$的上、下焦点分别为F1,F2,上焦点F1到直线 4x+3y+12=0的距离为3,椭圆C的离心率e=$\frac{1}{2}$.分析 (Ⅰ)利用点到直线的距离公式,即可求得c,利用椭圆的离心率,即可求得a的值,则b2=a2-c2,即可求得椭圆C的标准方程;
(Ⅱ)设直线方程,代入椭圆方程,求得B点坐标,根据向量数量积的坐标运算,求得H点坐标,利用两点之间的距离公式求得yM=1,联立MH及直线方程,即可求得直线l的方程.
解答 解:(Ⅰ)由已知椭圆方程为C:$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1({a>b>0})$,焦点在y轴上,
设椭圆上焦点F1(-c,0),由到直线4x+3y+12=0的距离为3,
得$\frac{丨3c+12丨}{5}$=3,
又椭圆的离心率e=$\frac{c}{a}$=$\frac{1}{2}$,则a=2c,
又a2=b2+c2,求得a2=4,b2=3.
椭圆方程为$\frac{{y}^{2}}{4}+\frac{{x}^{2}}{3}=1$;
(Ⅱ)设直线的斜率为k,则直线方程y-2=kx,设A(xA,yA),B(xB,yB),
由$\left\{\begin{array}{l}{y=kx+2}\\{\frac{{y}^{2}}{4}+\frac{{x}^{2}}{3}=1}\end{array}\right.$,得(3k2+4)x2+12kx=0,
则有xA=0,xB=-$\frac{12k}{3{k}^{2}+4}$,yB=$\frac{-6{k}^{2}+8}{3{k}^{2}+4}$,
所以$\overrightarrow{{F}_{1}B}$=(-$\frac{12k}{3{k}^{2}+4}$,$\frac{-6{k}^{2}+8}{3{k}^{2}+4}$-1),$\overrightarrow{{F}_{1}H}$=(xH,-1),
由$\overrightarrow{{F}_{1}B}$•$\overrightarrow{{F}_{1}H}$=0,
(-$\frac{12k}{3{k}^{2}+4}$)•xH+1-$\frac{-6{k}^{2}+8}{3{k}^{2}+4}$=0,
解得:xH=$\frac{9{k}^{2}-4}{12k}$,
由|${\overrightarrow{MO}}$|=|${\overrightarrow{MA}}$|,则xM2+yM2=xM2-(yM-2)2,yM=1,
MH方程:y=-$\frac{1}{k}$(x-$\frac{9{k}^{2}-4}{12k}$),
联立$\left\{\begin{array}{l}{y=kx+2}\\{y=-\frac{1}{k}(x-\frac{9{k}^{2}-4}{12k})}\end{array}\right.$,解得:yM=$\frac{9{k}^{2}+20}{12(1+{k}^{2})}$,
由yM=$\frac{9{k}^{2}+20}{12(1+{k}^{2})}$=1,解得:k2=$\frac{8}{3}$,k=±$\frac{2\sqrt{6}}{3}$,
∴直线l的方程y=±$\frac{2\sqrt{6}}{3}$x+2.
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,向量数量积的坐标运算,考查考查计算能力,属于中档题.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{5}{6}$ | C. | -$\frac{3}{4}$ | D. | $\frac{6}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线与x轴所成的夹角为30°,且双曲线的焦距为4$\sqrt{2}$.
已知椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线与x轴所成的夹角为30°,且双曲线的焦距为4$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 一次购物数量 | 1至2盒 | 3至5盒 | 6至9盒 | 10至17盒 | 18至25盒 |
| 顾客数量(人) | 20 | 14 | 10 | 2 | 4 |
| 结算的时间(分钟/人) | 1 | 1.5 | 2 | 1.5 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com