
分析 (1)f′(x)=ex-a,根据函数f(x)=ex-ax有极值1,可得存在x0,使得f′(x0)=${e}^{{x}_{0}}$-a=0,f(x0)=${e}^{{x}_{0}}$-ax0=1,解得x0,a.即可判断出结论.
(2)当x∈[0,+∞)时,f(x)≥mxln(x+1)+1恒成立?ex-x-1-mxln(x+1)≥0恒成立.令g(x)=ex-(x+1),x≥0.g(0)=0.利用导数研究其单调性可得:ex≥x+1.
①若mxln(x+1)+x+1≤x+1,则ex-x-1-mxln(x+1)≥0恒成立.可得:m≤0.
②m>0时,x≥0时,mxln(x+1)+x+1≤ex.令F(x)=mxln(x+1)+x+1-ex,(x≥0),F(0)=0.
由F(x)≤0,可得mxln(x+1)≤ex-x-1,x>0时,化为:m≤$\frac{{e}^{x}-x-1}{xln(x+1)}$.下面证明:$\frac{1}{2}$≤$\frac{{e}^{x}-x-1}{xln(x+1)}$.利用导数研究其单调性即可得出.
解答 解:(1)f′(x)=ex-a,∵函数f(x)=ex-ax有极值1,
∴存在x0,使得f′(x0)=${e}^{{x}_{0}}$-a=0,f(x0)=${e}^{{x}_{0}}$-ax0=1,
解得x0=0,a=1.
∴f′(x)=ex-1,可知:0是极小值点,因此1是极小值.
(2)当x∈[0,+∞)时,f(x)≥mxln(x+1)+1恒成立?ex-x-1-mxln(x+1)≥0恒成立.
令g(x)=ex-(x+1),x≥0.g(0)=0.
则g′(x)=ex-1≥0,
∴x≥0时,函数g(x)单调递增,因此g(x)≥g(0)=0,因此ex≥x+1.
①若mxln(x+1)+x+1≤x+1,则ex-x-1-mxln(x+1)≥0恒成立.
则mxln(x+1)≤0,可得:m≤0.
∴m≤0时,x≥0时,f(x)≥mxln(x+1)+1恒成立.
②m>0时,x≥0时,mxln(x+1)+x+1≤ex.
令F(x)=mxln(x+1)+x+1-ex,(x≥0),F(0)=0.
由F(x)≤0,可得mxln(x+1)≤ex-x-1,
x=0时,化为0≤0,恒成立,m∈R.
x>0时,化为:m≤$\frac{{e}^{x}-x-1}{xln(x+1)}$.
下面证明:$\frac{1}{2}$≤$\frac{{e}^{x}-x-1}{xln(x+1)}$.
令h(x)=2ex-2x-2-xln(x+1),h(0)=0.
h′(x)=2ex-2-ln(x+1)-$\frac{x}{x+1}$.h′(0)=0.
h″(x)=2ex-$\frac{1}{x+1}$-$\frac{1}{(x+1)^{2}}$≥h″(0)=0,
∴h′(x)≥0.
∴函数h(x)在[0,+∞)上单调递增,∴h(x)≥h(0)=0.
因此:$\frac{1}{2}$≤$\frac{{e}^{x}-x-1}{xln(x+1)}$成立,并且$\frac{1}{2}$是其最小值.
∴m≤$\frac{1}{2}$.
综上可得:实数m的取值范围是$(-∞,\frac{1}{2}]$.
点评 本题考查了利用导数研究函数的单调性极值与最值、分类讨论方法、方程与不等式的解法、等价转化方法,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
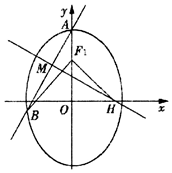 已知椭圆C:$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1({a>b>0})$的上、下焦点分别为F1,F2,上焦点F1到直线 4x+3y+12=0的距离为3,椭圆C的离心率e=$\frac{1}{2}$.
已知椭圆C:$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1({a>b>0})$的上、下焦点分别为F1,F2,上焦点F1到直线 4x+3y+12=0的距离为3,椭圆C的离心率e=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2+y2=5 | B. | x2+y2=3 | C. | x2+y2=9 | D. | x2+y2=7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
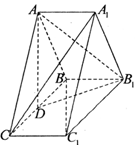 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,D为棱BC的中点,AB=AC,BC=$\sqrt{2}A{A_1}$,求证:
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,D为棱BC的中点,AB=AC,BC=$\sqrt{2}A{A_1}$,求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+$\sqrt{6}$ | B. | 1+$\sqrt{5}$ | C. | 1+$\sqrt{3}$ | D. | 1+$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 将一张边长为12cm的正方形纸片按如图(1)所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥模型,如图(2)所示放置.如果正四棱锥的主视图是等边三角形,如图(3)所示,则正四棱锥的体积是( )
将一张边长为12cm的正方形纸片按如图(1)所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥模型,如图(2)所示放置.如果正四棱锥的主视图是等边三角形,如图(3)所示,则正四棱锥的体积是( )| A. | $\frac{32}{3}$$\sqrt{6}$cm3 | B. | $\frac{64}{3}$$\sqrt{6}$cm3 | C. | $\frac{32}{3}$$\sqrt{2}$cm3 | D. | $\frac{64}{3}$$\sqrt{2}$cm3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com