
分析 (Ⅰ)求出函数的导数,通过讨论a的范围求出函数的单调区间即可;
(Ⅱ)求出x1,x2,得到f(x1)+f(x2)的解析式,问题转化为$ln[{(a-1)^2}]+\frac{2}{a-1}-2>0$,令a-1=t(a∈(0,1)∪(1,2)),所以t∈(-1,0)∪(0,1),令$g(t)=ln({t^2})+\frac{2}{t}-2$,根据函数的单调性判断即可;
(Ⅲ)问题转化为证明$ln(x+1)+\frac{1}{x+1}>\frac{1}{{{e^{x+1}}}}$,即证$lnx+\frac{1}{x}>\frac{1}{e^x}$,设$h(x)=lnx+\frac{1}{x}$,根据函数的单调性证明即可.
解答 解:(Ⅰ)$f'(x)=\frac{1}{x+1}+2a×[-\frac{1}{{{{(x+a)}^2}}}]=\frac{{{x^2}+a(a-2)}}{{(x+1){{(x+a)}^2}}}$,(*)
当a≥2时,∵x>0,∴$f'(x)=\frac{{{x^2}+a(a-2)}}{{(x+1){{(x+a)}^2}}}>0$,函数f(x)在(0,+∞)上是增函数;
当0<a<2时,由f'(x)=0,得x2+a(a-2)=0,解得${x_1}=-\sqrt{a(2-a)}$(负值舍去),${x_2}=\sqrt{a(2-a)}$,
所以当x∈(0,x2)时,x2+a(a-2)<0,从而f'(x)<0,函数f(x)在(0,x2)上是减函数;
当x∈(x2,+∞)时,x2+a(a-2)>0,从而f'(x)>0,函数f(x)在(x2,+∞)上是增函数.
综上,当a≥2时,函数f(x)在(0,+∞)上是增函数;
当0<a<2时,函数f(x)在$(0,\sqrt{a(2-a)})$上是减函数,在$(\sqrt{a(2-a)},+∞)$上是增函数.…(5分)
(Ⅱ)由(Ⅰ)知,当a≥2时,f'(x)>0,函数f(x)无极值点;
要使函数f(x)存在两个极值点,必有0<a<2,且极值点必为${x_1}=-\sqrt{a(2-a)}$,${x_2}=\sqrt{a(2-a)}$,
又由函数定义域知,x>-1,则有$-\sqrt{a(2-a)}>-1$,即$\sqrt{a(2-a)}<1$,化为(a-1)2>0,所以a≠1,
所以,函数f(x)存在两个极值点时,正数a的取值范围是(0,1)∪(1,2).
由(*)式可知,$\left\{\begin{array}{l}{x_1}+{x_2}=0\\{x_1}•{x_2}=a(a-2)\end{array}\right.$,
f(x1)+f(x2)
=ln(1+x1)+$\frac{2a}{{x}_{1}+a}$+ln(1+x2)+$\frac{2a}{{x}_{2}+a}$
=ln(1+x1+x2+x1•x2)+$\frac{2a{(x}_{1}{+x}_{2}+2a)}{{{x}_{1}x}_{2}+a{(x}_{1}{+x}_{2}){+a}^{2}}$
=ln[(a-1)2]+$\frac{{4a}^{2}}{a(a-2){+a}^{2}}$
=ln[(a-1)2]+$\frac{2}{a-1}$-2;
不等式f(x1)+f(x2)>4化为$ln[{(a-1)^2}]+\frac{2}{a-1}-2>0$,
令a-1=t(a∈(0,1)∪(1,2)),所以t∈(-1,0)∪(0,1),
令$g(t)=ln({t^2})+\frac{2}{t}-2$,t∈(-1,0)∪(0,1).
当t∈(-1,0)时,$g(t)=2ln(-t)+\frac{2}{t}-2$,$ln(-t)<0,\frac{2}{t}<0$,所以g(t)<0,不合题意;
当t∈(0,1)时,$g(t)=2lnt+\frac{2}{t}-2$,$g'(t)=2×\frac{1}{t}+2×(-\frac{1}{t^2})=\frac{2(t-1)}{t^2}<0$,
所以g(t)在(0,1)是减函数,所以$g(t)>g(1)=2ln1+\frac{2}{1}-2=0$,适合题意,即a∈(1,2).
综上,若f(x1)+f(x2)>4,此时正数a的取值范围是(1,2). …(10分)
(Ⅲ)证明:当a=1时,$f(x)=ln(x+1)+\frac{2}{x+1}$,
不等式$f(x)>\frac{1}{{{e^{x+1}}}}+\frac{1}{x+1}$可化为$ln(x+1)+\frac{1}{x+1}>\frac{1}{{{e^{x+1}}}}$,所以
要证不等式$f(x)>\frac{1}{{{e^{x+1}}}}+\frac{1}{x+1}$,即证$ln(x+1)+\frac{1}{x+1}>\frac{1}{{{e^{x+1}}}}$,即证$lnx+\frac{1}{x}>\frac{1}{e^x}$,
设$h(x)=lnx+\frac{1}{x}$,则$h'(x)=\frac{1}{x}-\frac{1}{x^2}=\frac{x-1}{x^2}$,
在(0,1)上,h'(x)<0,h(x)是减函数;
在£¨1£?+∞)上,h'(x)>0,h(x)是增函数.
所以h(x)≥h(1)=1,
设$ϕ(x)=\frac{1}{e^x}$,则ϕ(x)是减函数,
所以ϕ(x)<ϕ(0)=1,
所以ϕ(x)<h(x),即$lnx+\frac{1}{x}>\frac{1}{e^x}$,
所以当a=1时,不等式$f(x)>\frac{1}{{{e^{x+1}}}}+\frac{1}{x+1}$成立. …(14分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道综合题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
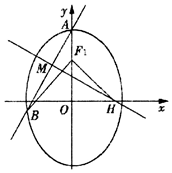 已知椭圆C:$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1({a>b>0})$的上、下焦点分别为F1,F2,上焦点F1到直线 4x+3y+12=0的距离为3,椭圆C的离心率e=$\frac{1}{2}$.
已知椭圆C:$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1({a>b>0})$的上、下焦点分别为F1,F2,上焦点F1到直线 4x+3y+12=0的距离为3,椭圆C的离心率e=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+$\sqrt{6}$ | B. | 1+$\sqrt{5}$ | C. | 1+$\sqrt{3}$ | D. | 1+$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com