
分析 可设△ABC的三边分别为a=5,b=7,c=8,运用余弦定理可得cosC,由同角的平方关系可得sinC,再由正弦定理可得该三角形的外接圆半径;由等面积可得内切圆半径.
解答 解:可设△ABC的三边分别为a=5,b=7,c=8,
由余弦定理可得,cosC=$\frac{25+49-64}{2×5×7}$=$\frac{1}{7}$,
可得sinC=$\frac{4\sqrt{3}}{7}$,
可得该三角形的外接圆半径为R=$\frac{1}{2}•\frac{8}{\frac{4\sqrt{3}}{7}}$=$\frac{{7\sqrt{3}}}{3}$,
由等面积可得$\frac{1}{2}(5+7+8)r=\frac{1}{2}×5×7×\frac{4\sqrt{3}}{7}$,
∴内切圆半径为$\sqrt{3}$.
故答案为$\frac{{7\sqrt{3}}}{3}$,$\sqrt{3}$.
点评 本题考查三角形的外接圆的半径、内切圆半径的求法,注意运用正弦定理和余弦定理,考查运算能力,属于基础题.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:解答题
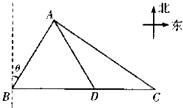 如图,某流动海洋观测船开始位于灯塔B的北偏东$θ(0<θ<\frac{π}{2})$方向,且满足$2{sin^2}(\frac{π}{4}+θ)-\sqrt{3}$cos2θ=1,AB=AD,在接到上级命令后,该观测船从A点位置沿AD方向在D点补充物资后沿BD方向在C点投放浮标,使得C点与A点的距离为4$\sqrt{3}$km,
如图,某流动海洋观测船开始位于灯塔B的北偏东$θ(0<θ<\frac{π}{2})$方向,且满足$2{sin^2}(\frac{π}{4}+θ)-\sqrt{3}$cos2θ=1,AB=AD,在接到上级命令后,该观测船从A点位置沿AD方向在D点补充物资后沿BD方向在C点投放浮标,使得C点与A点的距离为4$\sqrt{3}$km,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=|x|,g(x)=$\sqrt{{x}^{2}}$ | B. | f(x)=$\sqrt{{x}^{2}}$,g(x)=($\sqrt{x}$)2 | ||
| C. | f(x)=$\frac{{x}^{2}-1}{x-1}$,g(x)=x+1 | D. | f(x)=$\sqrt{x+1}$,g(x)=$\sqrt{{x}^{2}-1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com