
(1)设x≥1,y≥1,证明x+y+ ≤
≤ +
+ +xy;
+xy;
(2)1<a≤b≤c,证明logab+logbc+logca≤logba+logcb+logac.
(1)见解析(2)见解析
【解析】(1)由于x≥1,y≥1,
要证x+y+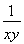 ≤
≤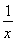 +
+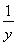 +xy,
+xy,
只需证xy(x+y)+1≤y+x+(xy)2.
因为[y+x+(xy)2]-[xy(x+y)+1]
=[(xy)2-1]-[xy(x+y)-(x+y)]
=(xy+1)(xy-1)-(x+y)(xy-1)
=(xy-1)(xy-x-y+1)
=(xy-1)(x-1)(y-1).
由条件x≥1,y≥1,得(xy-1)(x-1)(y-1)≥0,
从而所要证明的不等式成立.
(2)设logab=x,logbc=y,由对数的换底公式得logca=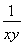 ,logba=
,logba=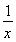 ,logcb=
,logcb= ,logac=xy.
,logac=xy.
于是,所要证明的不等式即为x+y+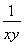 ≤
≤ +
+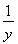 +xy.
+xy.
其中x=logab≥1,y=logbc≥1.
故由(1)可知所要证明的不等式成立.


科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集14讲练习卷(解析版) 题型:选择题
已知双曲线 =1(a>0,b>0)的一个焦点到渐近线的距离是焦距的
=1(a>0,b>0)的一个焦点到渐近线的距离是焦距的 ,则双曲线的离心率是( )
,则双曲线的离心率是( )
A.2 B.4 C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集11讲练习卷(解析版) 题型:选择题
某四棱锥的底面为正方形,其三视图如图所示,则该四棱锥的体积等于( )

A.1 B.2 C.3 D.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集10讲练习卷(解析版) 题型:选择题
若数列{cn}的通项cn=(2n-1)· ,则数列{cn}的前n项和Rn=( )
,则数列{cn}的前n项和Rn=( )
A.1- B.1-
B.1- C.1+
C.1+ D.1+
D.1+
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试选修4-5不等式选讲练习卷(解析版) 题型:解答题
已知a,b为正实数.
(1)求证: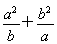 ≥a+b;
≥a+b;
(2)利用(1)的结论求函数y=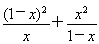 (0<x<1)的最小值.?
(0<x<1)的最小值.?
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试选修4-5不等式选讲 练习卷(解析版) 题型:填空题
已知a,b,c∈R,a+2b+3c=6,则a2+4b2+9c2的最小值为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试选修4-5不等式选讲 练习卷(解析版) 题型:选择题
“a<4”是“对任意的实数x,|2x-1|+|2x+3|≥a成立”的( )
A.充分必要条件 B.充分不必要条件
C.必要不充分条件 D.既非充分也非必要条件
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试选修4-1几何证明选讲练习卷(解析版) 题型:解答题
如图,AB为⊙O的直径,直线CD与⊙O相切于E,AD垂直CD于D,BC垂直CD于C,EF垂直AB于F,连接AE,BE.证明:

(1)∠FEB=∠CEB;
(2)EF2=AD·BC.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(六)第二章第三节练习卷(解析版) 题型:填空题
已知y=f(x)+x2是奇函数,且f(1)=1,若g(x)=f(x)+2,则g(-1)= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com