
分析 展开$\overrightarrow{a}$•($\overrightarrow{a}$+$\overrightarrow{b}$)=8,代入数量积公式求得答案.
解答 解:∵$\overrightarrow{a}$•($\overrightarrow{a}$+$\overrightarrow{b}$)=8,且|$\overrightarrow{a}$|=2,$<\overrightarrow{a},\overrightarrow{b}>=\frac{π}{3}$,
∴${\overrightarrow{a}}^{2}+\overrightarrow{a}•\overrightarrow{b}=8$,即$|\overrightarrow{a}{|}^{2}+|\overrightarrow{a}||\overrightarrow{b}|•cos<\overrightarrow{a},\overrightarrow{b}>=8$,
∴${2}^{2}+2|\overrightarrow{b}|×\frac{1}{2}=8$,
解得:$|\overrightarrow{b}|=1$.
故答案为:1.
点评 本题考查平面向量的数量积运算,关键是对数量积公式的记忆,是中档题.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高一上学期月考一数学试卷(解析版) 题型:解答题
已知函数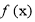 的定义域为
的定义域为 ,对于任意的
,对于任意的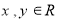 ,都有
,都有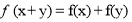 ,且当
,且当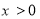 时,
时, ,若
,若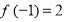 .
.
(1) 求证: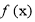 是
是 上的减函数;
上的减函数;
(2) 求函数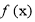 在区间
在区间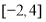 上的值域.
上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-$\frac{1}{24}$ | B. | x=-$\frac{1}{24}$ | C. | x=-$\frac{3}{2}$ | D. | y=-$\frac{3}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com