Question

13．已知抛物线C：x²=4y的焦点为F，C的准线和对称轴交于点M，点P是C上一点，且满足|PM|=λ|PF|，当λ取最大值时，点P恰好在以M、F为焦点的双曲线上，则双曲线的离心率为$\sqrt{2}$+1．

Answer 1

分析 过P作准线的垂线，垂足为N，则由抛物线的定义，结合|PM|=λ|PF|，可得$\frac{|PN|}{|PA|}$=$\frac{1}{λ}$，设PA的倾斜角为α，则当λ取得最大值时，sinα最小，此时直线PM与抛物线相切，求出P的坐标，利用双曲线的定义，即可求得双曲线的离心率．

解答 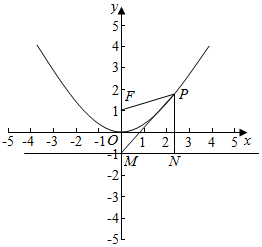解：过P作准线的垂线，垂足为N，
则由抛物线的定义可得|PN|=|PF|，
∵|PM|=λ|PF|，∴|PM|=λ|PN|，则$\frac{|PN|}{|PA|}$=$\frac{1}{λ}$，
设PM的倾斜角为α，则sinα=$\frac{1}{λ}$，
当λ取得最大值时，sinα最小，此时直线PM与抛物线相切，
设直线PM的方程为y=kx-1，代入x²=4y，可得x²=4（kx-1），
即x²-4kx+4=0，
∴△=16k²-16=0，∴k=±1，
∴P（2，1），
∴双曲线的实轴长为|PM|-|PF|=2（$\sqrt{2}$-1），
∴双曲线的离心率为$\frac{2}{2（\sqrt{2}-1）}$=$\sqrt{2}$+1．
故答案为：$\sqrt{2}$+1．

点评 本题考查抛物线的性质，考查双曲线、抛物线的定义，考查学生分析解决问题的能力，解答此题的关键是明确当λ取得最大值时，sinα最小，此时直线PA与抛物线相切，属中档题．