
| A. | (-1,-$\frac{1}{2}$) | B. | (0,$\frac{1}{2}$) | C. | (-$\frac{1}{2}$,0) | D. | ($\frac{1}{2},1$) |
分析 由题意,可知f(x)-xeX是定值,令t=f(x)-xeX,得出f(x)=xeX+t,再由f(t)=tet+t=0求出t的值,即可得出f(x)的表达式,求出函数的导数,即可求出f(x)-f′(x)=x的解所在的区间,即得正确选项.
解答 解:由题意,可知f(x)-xeX是定值,不妨令t=f(x)-xeX,则f(x)=xeX+t,
又f(t)=tet+t=0,解得t=0,
所以有f(x)=xeX,
所以f′(x)=(x+1)eX,
令F(x)=f(x)-f′(x)-x=xex-(x+1)ex-x=-ex-x,
可得F(-1)=1-$\frac{1}{e}$>0,F(-$\frac{1}{2}$)=$\frac{1}{2}$-$\frac{\sqrt{e}}{e}$<0
即F(x)的零点在区间(-1,-$\frac{1}{2}$)内
∴方程f(x)-f′(x)=x的解所在的区间是(-1,-$\frac{1}{2}$),
故选:A.
点评 本题考查导数运算法则,函数的零点,解题的关键是判断出f(x)-xex是定值,本题考查了转化的思想,将方程的根转化为函数的零点来进行研究,降低了解题的难度.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(理)试卷(解析版) 题型:解答题
已知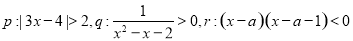 .
.
(1)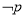 是
是 的什么条件?
的什么条件?
(2)若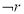 是
是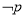 的必要非充分条件,求实数
的必要非充分条件,求实数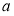 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高一上学期月考一数学试卷(解析版) 题型:解答题
已知函数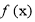 的定义域为
的定义域为 ,对于任意的
,对于任意的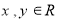 ,都有
,都有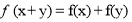 ,且当
,且当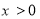 时,
时, ,若
,若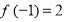 .
.
(1) 求证: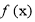 是
是 上的减函数;
上的减函数;
(2) 求函数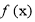 在区间
在区间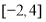 上的值域.
上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,3x+3-x>2 | B. | ?x∈R,3x+3-x≤2 | C. | ?x∈R,3x+3-x≤2 | D. | ?x∈R,3x+3-x<2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com