
分析 (Ⅰ)求f(x)的定义域,函数的导数,通过k的范围讨论,导函数的符号,求解函数的单调区间;
(Ⅱ)借助(Ⅰ),利用函数的单调性以及最小值的符号,判断f(x)在$(1,\sqrt{e}]$存在零点的条件,列出不等式求k的取值范围.
解答 解:(I)f(x)的定义域为(0,+∞)…1分
${f^'}(x)=x-\frac{k}{x}=\frac{{{x^2}-k}}{x}$.…2分
(1)k≤0时,f′(x)>0,f(x)在(0,+∞)上单调递增…3分
(2)k>0时,由f′(x)=0解得$x=\sqrt{k}$.f(x)与f′(x)在区间f(0)<1上的情况如下:
| x | (0,$\sqrt{k}$) | $\sqrt{k}$ | ($\sqrt{k}$,+∞) |
| f′(x) | - | 0 | + |
| f(x) | ↓ | $\frac{k(1-lnk)}{2}$ | ↑ |
点评 本题考查函导数的综合应用.函数的单调性以及函数的最值,函数的零点,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:解答题
 已知函数f(x)=2sin(2ωx+$\frac{π}{6}$)(其中0<ω<1),若点(-$\frac{π}{6}$,0)是函数f(x)图象的一个对称中心.
已知函数f(x)=2sin(2ωx+$\frac{π}{6}$)(其中0<ω<1),若点(-$\frac{π}{6}$,0)是函数f(x)图象的一个对称中心.查看答案和解析>>
科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(理)试卷(解析版) 题型:解答题
已知函数 的图像
的图像 在点
在点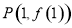 处切线的斜率为
处切线的斜率为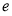 ,记奇函数
,记奇函数 的图像为
的图像为 .
.
(1)求实数 的值;
的值;
(2)当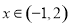 时,图像
时,图像 恒在
恒在 的上方,求实数
的上方,求实数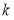 的取值范围;
的取值范围;
(3)若图像 与
与 有两个不同的交点
有两个不同的交点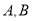 ,其横坐标分别是
,其横坐标分别是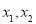 ,设
,设 ,求证:
,求证: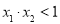 .[来
.[来
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,-$\frac{1}{2}$) | B. | (0,$\frac{1}{2}$) | C. | (-$\frac{1}{2}$,0) | D. | ($\frac{1}{2},1$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
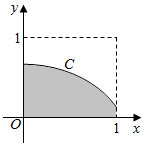 在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为( )
在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为( )| A. | 2386 | B. | 2718 | C. | 3413 | D. | 4772 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com