
分析 (1)把a=-1代入函数解析式,求出内函数g(x)=-x2-4x+3的单调区间,结合复合函数的单调性求得f(x)的单调区间;
(2)由指数函数的性质知,要使y=f(x)的值域是(0,+∞),应使h(x)=ax2-4x+3的值域为R,由此可得a的值.
解答 解:(1)当a=-1时,$f(x)=(\frac{1}{3})^{-{x}^{2}-4x+3}$.
令g(x)=-x2-4x+3,由于g(x)在(-∞,-2)上单调递增,在(-2,+∞)上单调递减,
而y=$(\frac{1}{3})^{t}$在R上单调递减,
∴f(x)的增区间为(-2,+∞),减区间为(-∞,-2);
(2)由指数函数的性质知,要使y=f(x)的值域是(0,+∞),
应使h(x)=ax2-4x+3的值域为R,
若a≠0,h(x)为二次函数,其值域不可能为R,
∴a的值是0.
点评 本题考查复合函数单调性的求法,考查了复合函数的值域,是中档题.


科目:高中数学 来源: 题型:解答题
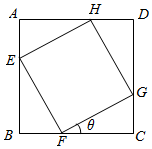 如图所示,有块正方形的钢板ABCD,其中一个角有部分损坏,现要把它截成一块正方形的钢板EFGH.在直角三角形GFC中,∠GFC=θ.若截后的正方形钢板EFGH的面积是原正方形ABCD的面积的三分之二,求θ的值.
如图所示,有块正方形的钢板ABCD,其中一个角有部分损坏,现要把它截成一块正方形的钢板EFGH.在直角三角形GFC中,∠GFC=θ.若截后的正方形钢板EFGH的面积是原正方形ABCD的面积的三分之二,求θ的值.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 39 | B. | 42 | C. | 48 | D. | 56 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∨(¬q) | C. | p∧(¬q) | D. | (¬p)∧q |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com