
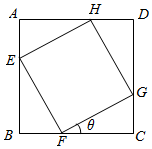
 如图所示,有块正方形的钢板ABCD,其中一个角有部分损坏,现要把它截成一块正方形的钢板EFGH.在直角三角形GFC中,∠GFC=θ.若截后的正方形钢板EFGH的面积是原正方形ABCD的面积的三分之二,求θ的值.
如图所示,有块正方形的钢板ABCD,其中一个角有部分损坏,现要把它截成一块正方形的钢板EFGH.在直角三角形GFC中,∠GFC=θ.若截后的正方形钢板EFGH的面积是原正方形ABCD的面积的三分之二,求θ的值. 分析 设AB=1,设CG=a,则CF=1-a,计算FG,根据面积比列方程解出a,得出CG,CF,得出θ的值.
解答 解:设正方形ABCD的边长为1,CG=a,则BF=CG=a,CF=1-a,
∴FG=$\sqrt{C{F}^{2}+C{G}^{2}}$=$\sqrt{2{a}^{2}-2a+1}$.
∴正方形EFGH的面积S=FG2=2a2-2a+1=$\frac{2}{3}$.
解得a=$\frac{1}{2}±\frac{\sqrt{3}}{6}$.
∴CG=$\frac{1}{2}+\frac{\sqrt{3}}{6}$,CF=$\frac{1}{2}-\frac{\sqrt{3}}{6}$,或者CG=$\frac{1}{2}-\frac{\sqrt{3}}{6}$,CF=$\frac{1}{2}+\frac{\sqrt{3}}{6}$.
∴tanθ=$\frac{CG}{CF}$=2+$\sqrt{3}$或2-$\sqrt{3}$.
∴θ=arctan(2+$\sqrt{3}$)或θ=arctan(2-$\sqrt{3}$).
点评 本题考查了解三角形的实际应用,属于基础题.


 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (-2,1) | B. | (-2,1] | C. | (1,2) | D. | [1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{17}{18}$ | B. | -$\frac{17}{18}$ | C. | $\frac{18}{17}$ | D. | -$\frac{18}{17}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com