
分析 利用同角三角函数的基本关系、以及三角函数在各个象限中的符号,求得cosα和cos(α+β)的值,再利用两角和差的三角公式求得 cosβ=cos[(α+β)-α]的值.
解答 解:∵sinα=$\frac{3}{5}$,sin(α+β)=$\frac{5}{13}$(α,β为第一象限角),∴cosα=$\sqrt{{1-sin}^{2}α}$=$\frac{4}{5}$,sinα>sin(α+β),
∴α+β∈($\frac{π}{2}$,π),∴cos(α+β)=-$\sqrt{{1-sin}^{2}(α+β)}$=-$\frac{12}{13}$,
∴cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα=-$\frac{12}{13}$•$\frac{4}{5}$+$\frac{5}{13}$•$\frac{3}{5}$=-$\frac{33}{65}$.
点评 本题主要考查同角三角函数的基本关系、以及三角函数在各个象限中的符号,两角和差的三角公式的应用,属于基础题.


 小学教材全测系列答案
小学教材全测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{1}{3}$ | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
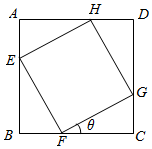 如图所示,有块正方形的钢板ABCD,其中一个角有部分损坏,现要把它截成一块正方形的钢板EFGH.在直角三角形GFC中,∠GFC=θ.若截后的正方形钢板EFGH的面积是原正方形ABCD的面积的三分之二,求θ的值.
如图所示,有块正方形的钢板ABCD,其中一个角有部分损坏,现要把它截成一块正方形的钢板EFGH.在直角三角形GFC中,∠GFC=θ.若截后的正方形钢板EFGH的面积是原正方形ABCD的面积的三分之二,求θ的值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(理)试卷(解析版) 题型:解答题
根据统计资料,某工艺品厂的日产量最多不超过20件根据统计资料,每日产品废品率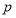 与日产量
与日产量 (件)之间近似地满足关系式
(件)之间近似地满足关系式 (日产品废品率=
(日产品废品率= ×100%) .
×100%) .
已知每生产一件正品可赢利2千元,而生产一件废品则亏损1千元.(该车间的日利润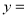 日正品赢利额
日正品赢利额 日废品亏损额)
日废品亏损额)
(1)将该车间日利润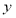 (千元)表示为日产量
(千元)表示为日产量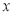 (件)的函数;
(件)的函数;
(2)当该车间的日产量为多少件时,日利润最大?最大日利润是几千元?
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高一上学期月考一数学试卷(解析版) 题型:解答题
已知函数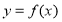 是定义在
是定义在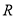 上的奇函数,当
上的奇函数,当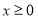 时,
时, .
.
(1)求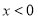 时
时 的解析式;
的解析式;
(2)问是否存在正数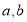 ,当
,当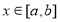 时,
时,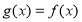 ,且
,且 的值域为
的值域为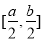 ?若存
?若存
在,求出所有的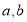 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com