
分析 由正弦定理化简后设a=4k、b=5k、c=7k(k>0),由余弦定理求出cosB的值,根据中线AM和余弦定理列出方程,求出k的值即可求出AC.
解答 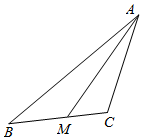 解:∵sinA:sinB:sinC=4:5:7,
解:∵sinA:sinB:sinC=4:5:7,
∴由正弦定理得,a:b:c=4:5:7,不妨设a=4k、b=5k、c=7k(k>0),
由余弦定理得,cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{{16k}^{2}+49{k}^{2}-25{k}^{2}}{2×4k×7k}$=$\frac{5}{7}$,
∵点M为BC的中点,AM=$\sqrt{11}$,
∴由余弦定理得,AM2=BA2+BM2-2BA•BM•cosB,
∴11=$49{k}^{2}+4{k}^{2}-2×7k×2k×\frac{5}{7}$,解得k=$\frac{\sqrt{3}}{3}$,
∴AC=b=$\frac{{5\sqrt{3}}}{3}$,
故答案为:$\frac{{5\sqrt{3}}}{3}$.
点评 本题考查正弦定理、余弦定理的综合应用,以及方程思想,属于中档题.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:选择题
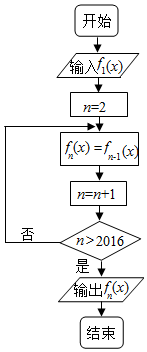 执行如图的程序框图,当n≥2,n∈N*时,fn(x)表示fn-1(x)的导函数,若输入函数f1(x)=sinx-cosx,则输出的函数fn(x)可化为( )
执行如图的程序框图,当n≥2,n∈N*时,fn(x)表示fn-1(x)的导函数,若输入函数f1(x)=sinx-cosx,则输出的函数fn(x)可化为( )| A. | $\sqrt{2}$sin(x+$\frac{π}{4}}$) | B. | $\sqrt{2}$sin(x-$\frac{π}{4}}$) | C. | -$\sqrt{2}$sin(x+$\frac{π}{4}}$) | D. | -$\sqrt{2}$sin(x-$\frac{π}{4}}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,1) | B. | (-2,1] | C. | (1,2) | D. | [1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
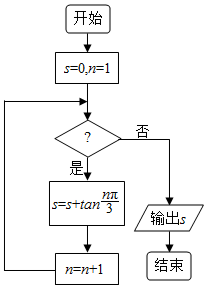 阅读如图所示的程序框图,若运行相应的程序输出的结果为0,则判断框中的条件不可能是( )
阅读如图所示的程序框图,若运行相应的程序输出的结果为0,则判断框中的条件不可能是( )| A. | n≤2014 | B. | n≤2015 | C. | n≤2016 | D. | n≤2018 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
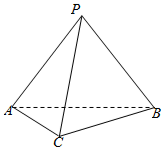 如图,在三棱锥P-ABC中,底面ABC为直角三角形,且∠ACB=90°,∠ABC=30°,AB=2,侧面PAB为等边三角形.
如图,在三棱锥P-ABC中,底面ABC为直角三角形,且∠ACB=90°,∠ABC=30°,AB=2,侧面PAB为等边三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com