
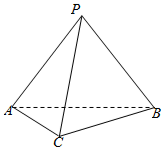
 如图,在三棱锥P-ABC中,底面ABC为直角三角形,且∠ACB=90°,∠ABC=30°,AB=2,侧面PAB为等边三角形.
如图,在三棱锥P-ABC中,底面ABC为直角三角形,且∠ACB=90°,∠ABC=30°,AB=2,侧面PAB为等边三角形.分析 (I)计算AC,PA,利用勾股定理的逆定理得出AC⊥PC,结合AC⊥BC得出AC⊥平面PBC,于是AC⊥PB;'
(II)取AB中点O,连结OP,求出S△ABC,OP,S△PBC,根据等体积法得出三棱锥A-PBC的高.
解答 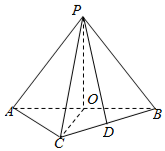 证明:(Ⅰ)∵∠ACB=90°,∠ABC=30°,AB=2,∴AC=1,BC=$\sqrt{3}$
证明:(Ⅰ)∵∠ACB=90°,∠ABC=30°,AB=2,∴AC=1,BC=$\sqrt{3}$
∵△PAB是等边三角形,∴PA=AB=2,
∴当$PC=\sqrt{3}$时,AC2+PC2=PA2,∴AC⊥PC.
又AC⊥BC,PC?平面PBC,BC?平面PBC,CB∩PC=C,
∴AC⊥平面PBC,又PB?平面PBC,
∴AC⊥PB.
(Ⅱ)取AB中点O,连接PO,CO,则PO⊥AB,
∵平面PAB⊥平面ABC=AB,PO⊥AB,PO?平面PAB,
∴PO⊥平面ABC,∴PO⊥OC,
∵△ABC是直角三角形,△PAB是等边三角形,AB=2,O是AB的中点,
∴OC=$\frac{1}{2}AB$=1,OP=$\sqrt{3}$,
∴$PC=\sqrt{P{O^2}+O{C^2}}=\sqrt{3+1}=2$,
∴PB=PC=2,作PD⊥BC于D,则D为BC的中点,BD=$\frac{1}{2}BC$=$\frac{\sqrt{3}}{2}$.
∴PD=$\sqrt{P{B}^{2}-B{D}^{2}}$=$\frac{\sqrt{13}}{2}$.
∴${S_{△PBC}}=\frac{1}{2}×\sqrt{3}×\frac{{\sqrt{13}}}{2}=\frac{{\sqrt{39}}}{4}$.
又${S_{△ABC}}=\frac{1}{2}×1×\sqrt{3}=\frac{{\sqrt{3}}}{2}$,
∵VP-ABC=$\frac{1}{3}{S}_{△ABC}•OP$,
设三棱锥A-PBC的高为h,则VA-PBC=$\frac{1}{3}{S}_{△PBC}•h$
∴$h=\frac{{\frac{1}{3}×{S_{△ABC}}×OP}}{{\frac{1}{3}×{S_{△PBC}}}}=\frac{{\frac{{\sqrt{3}}}{2}×\sqrt{3}}}{{\frac{{\sqrt{39}}}{4}}}=\frac{{2\sqrt{39}}}{13}$.
点评 本题考查了线面垂直的判定与性质,棱锥的体积计算,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{2}$个单位 | B. | 向左平移$\frac{π}{2}$个单位 | ||
| C. | 向右平移$\frac{π}{4}$个单位 | D. | 向左平移$\frac{π}{4}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{1}{3}$ | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高一上学期月考一数学试卷(解析版) 题型:解答题
已知函数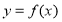 是定义在
是定义在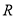 上的奇函数,当
上的奇函数,当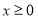 时,
时, .
.
(1)求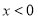 时
时 的解析式;
的解析式;
(2)问是否存在正数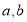 ,当
,当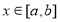 时,
时,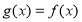 ,且
,且 的值域为
的值域为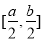 ?若存
?若存
在,求出所有的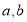 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com