
| A. | 向右平移$\frac{π}{2}$个单位 | B. | 向左平移$\frac{π}{2}$个单位 | ||
| C. | 向右平移$\frac{π}{4}$个单位 | D. | 向左平移$\frac{π}{4}$个单位 |
分析 利用三角函数恒等变换的应用对函数化简,根据周期公式求ω的值,从而可求f(x),进而根据函数y=Asin(ωx+φ)的图象变换规律,即可得解.
解答 解:∵$f(x)=2sinωxcos(ωx+\frac{π}{3})$
=$2sinωx(\frac{1}{2}cosωx-\frac{{\sqrt{3}}}{2}sinωx)$
=$sinωxcosωx-\sqrt{3}{sin^2}ωx$
=$\frac{1}{2}sin2ωx+\frac{{\sqrt{3}}}{2}cos2ωx-\frac{{\sqrt{3}}}{2}$
=$sin(2ωx+\frac{π}{3})-\frac{{\sqrt{3}}}{2}$.
由题意知f(x)的最小正周期为T=π,则ω=1,
∴$f(x)=sin(2x+\frac{π}{3})-\frac{{\sqrt{3}}}{2}$,
∵$f(x+\frac{π}{4})=sin[2(x+\frac{π}{4})+\frac{π}{3}]-\frac{{\sqrt{3}}}{2}=sin(2x+\frac{π}{3}+\frac{π}{2})-\frac{{\sqrt{3}}}{2}=cos(2x+\frac{π}{3})-\frac{{\sqrt{3}}}{2}$,
∴要得到函数$y=cos(2x+\frac{π}{3})-\frac{{\sqrt{3}}}{2}$的图象,只需将函数y=f(x)的图象向左平移$\frac{π}{4}$个单位.
故选:D.
点评 本题主要考查了函数y=Asin(ωx+φ)的图象变换,考查了利用三角函数恒等变换的应用把不同名的三角函数化为一个角的三角函数,进而研究三角函数的性质,属于中档题.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | (-2,1) | B. | (-2,1] | C. | (1,2) | D. | [1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
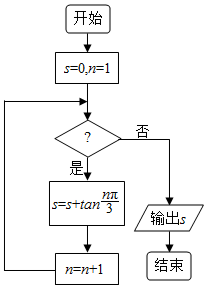 阅读如图所示的程序框图,若运行相应的程序输出的结果为0,则判断框中的条件不可能是( )
阅读如图所示的程序框图,若运行相应的程序输出的结果为0,则判断框中的条件不可能是( )| A. | n≤2014 | B. | n≤2015 | C. | n≤2016 | D. | n≤2018 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
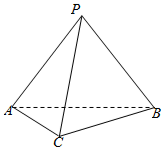 如图,在三棱锥P-ABC中,底面ABC为直角三角形,且∠ACB=90°,∠ABC=30°,AB=2,侧面PAB为等边三角形.
如图,在三棱锥P-ABC中,底面ABC为直角三角形,且∠ACB=90°,∠ABC=30°,AB=2,侧面PAB为等边三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com