
分析 设出E点的坐标,表示出$\overrightarrow{OA}$+$\overrightarrow{OB}$的模,结合三角函数的性质求出最小值即可.
解答 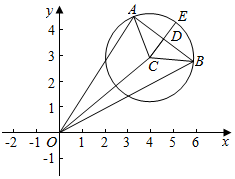 解:设AB的中点为D,则CD=1,
解:设AB的中点为D,则CD=1,
延长CD交圆C于点E,则D为CE的中点,
∵$|{\overrightarrow{OA}+\overrightarrow{OB}}|=|{\overrightarrow{OC}+\overrightarrow{CA}+\overrightarrow{OC}+\overrightarrow{CB}}|$=$|{2\overrightarrow{OC}+\overrightarrow{CE}}|$,
设E(4+2cosθ,3+2sinθ),
∴$|{\overrightarrow{OA}+\overrightarrow{OB}}|=|{(8,6)+(2cosθ,2sinθ)}|$
=|(8+2cosθ,6+2sinθ)|
=$\sqrt{{{(8+2cosθ)}^2}+{{(6+2sinθ)}^2}}$
=$\sqrt{104+8(3sinθ+4cosθ)}$
=$\sqrt{104+40sin(θ+φ)}≥\sqrt{104-40}=8$.
点评 本题考查了向量的运算,考查三角函数问题,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | (x-1)2+y2=4 | B. | (x-2)2+y2=4 | C. | (x-1)2+y2=8 | D. | (x-2)2+y2=8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有最大值2,无最小值 | B. | 有最小值2,无最大值 | ||
| C. | 有最小值$\frac{1}{2}$,最大值2 | D. | 既无最小值,也无最大值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
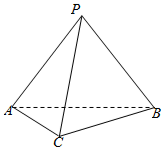 如图,在三棱锥P-ABC中,底面ABC为直角三角形,且∠ACB=90°,∠ABC=30°,AB=2,侧面PAB为等边三角形.
如图,在三棱锥P-ABC中,底面ABC为直角三角形,且∠ACB=90°,∠ABC=30°,AB=2,侧面PAB为等边三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,+∞) | B. | (-2,+∞) | C. | (2,+∞) | D. | (3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{9}{20}$ | D. | $\frac{19}{20}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com