
| A. | (0,$\frac{1}{e}$) | B. | (0,1) | C. | ($\frac{1}{e}$,1) | D. | (0,$\frac{1}{e}$] |
分析 令f(x)=0,即为方程|xex|=t有三个不相等的实数解,即y=t与函数y=|xex|的图象有三个交点,利用导数法分析g(x)=xex的单调性和极值,进而结合函数图象的对折变换画出函数y=|xex|的图象,数形结合可得答案.
解答 解:令f(x)=0,即为|xex|=t,
令g(x)=xex,则g′(x)=(1+x)ex,
当x<-1时,g′(x)<0,当x>-1时,g′(x)>0,
故g(x)=xex在(-∞,-1)上为减函数,在(-1,+∞)上是减函数,
g(-1)=-$\frac{1}{e}$,
又由x<0时,g(x)<0,当x>0时,g(x)>0,
故函数y=|xex|的图象如下图所示:
故当t∈(0,$\frac{1}{e}$)时,y=t与函数y=|xex|的图象有三个交点,
即方程|xex|=t有三个不相等的实数解,
故t的取值范围是(0,$\frac{1}{e}$),
故选:A.
点评 本题考查的知识点是零点的存在性及零点的个数,其中结合函数图象的对折变换画出函数y=|xex|的图象,是解答的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 几何体 | 代数题 | 总计 | |
| 男同学 | 22 | 8 | 30 |
| 女同学 | 8 | 12 | 20 |
| 总计 | 30 | 20 | 50 |
| P(k2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.10 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.481 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{3}$ | B. | $\frac{3π}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
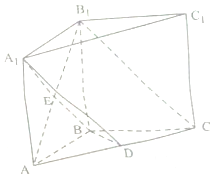 如图,在直三棱柱ABC-A1B1C1中,AB=BC=BB1,AB1∩A1B=E,D为AC上的点,B1C∥平面A1BD.
如图,在直三棱柱ABC-A1B1C1中,AB=BC=BB1,AB1∩A1B=E,D为AC上的点,B1C∥平面A1BD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com