
已知椭圆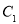 的中心在原点、焦点在
的中心在原点、焦点在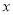 轴上,抛物线
轴上,抛物线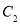 的顶点在原点、焦点在
的顶点在原点、焦点在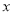 轴上.小明从曲线
轴上.小明从曲线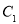 、
、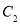 上各取若干个点(每条曲线上至少取两个点),并记录其坐标(
上各取若干个点(每条曲线上至少取两个点),并记录其坐标( .由于记录失误,使得其中恰有一个点既不在椭圆
.由于记录失误,使得其中恰有一个点既不在椭圆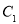 上,也不在抛物线
上,也不在抛物线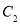 上,小明的记录如下:
上,小明的记录如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
据此,可推断抛物线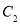 的方程为_____________.
的方程为_____________.
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源:2015届福建省高二下学期期末考理科数学试卷(解析版) 题型:解答题
甲、乙两台机床生产同一型号零件.记生产的零件的尺寸为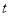 (cm),相关行业质检部门规定:若
(cm),相关行业质检部门规定:若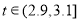 ,则该零件为优等品;若
,则该零件为优等品;若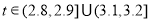 ,则该零件为中等品;其余零件为次品.现分别从甲、乙机床生产的零件中各随机抽取50件,经质量检测得到下表数据:
,则该零件为中等品;其余零件为次品.现分别从甲、乙机床生产的零件中各随机抽取50件,经质量检测得到下表数据:
尺寸 |
|
|
|
|
|
|
甲零件频数 | 2 | 3 | 20 | 20 | 4 | 1 |
乙零件频数 | 3 | 5 | 17 | 13 | 8 | 4 |
(Ⅰ)设生产每件产品的利润为:优等品3元,中等品1元,次品亏本1元.若将频率视为概率,试根据样本估计总体的思想,估算甲机床生产一件零件的利润的数学期望;
(Ⅱ)对于这两台机床生产的零件,在排除其它因素影响的情况下,试根据样本估计总体的思想,估计约有多大的把握认为“零件优等与否和所用机床有关”,并说明理由.
参考公式: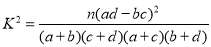 .
.
参考数据:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二上学期期中考试理科数学试卷(解析版) 题型:解答题
已知椭圆的一个顶点为 ,焦点在
,焦点在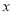 轴上,若右焦点到直线
轴上,若右焦点到直线 的距离为
的距离为 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)是否存在斜率为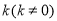 ,且过定点
,且过定点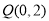 的直线
的直线 ,使
,使 与椭圆交于两个不同的点
与椭圆交于两个不同的点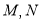 ,且
,且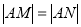 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二上学期期中考试理科数学试卷(解析版) 题型:选择题
以下茎叶图记录了甲.乙两组各五名学生在一次英语听力测试中的成绩(单位:分)
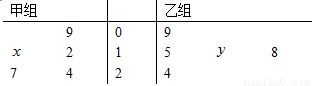
已知甲组数据的中位数为5,乙组数据的平均数为6.8,则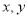 的值分别为
的值分别为
A.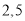 B.
B.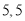 C.
C.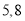 D.
D.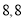
查看答案和解析>>
科目:高中数学 来源:2015届福建省晋江市高二下学期期末理科数学试卷(解析版) 题型:选择题
在某种信息传输过程中,用4个数字的一个排列(数字允许重复)表示一个信息,不同排列表示不同信息.若所用数字只有0和1,则与信息0110至多有两个对应位置上的数字相同的信息个数为 ( )
A.10 B.11 C.12 D.15
查看答案和解析>>
科目:高中数学 来源:2015届福建省等三校高二下学期期末理科数学试卷(解析版) 题型:填空题
将三个分别标有A,B,C的球随机放入编号为1,2,3,4的四个盒子中,则1号盒子中有球的不同放法种数为______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com