分析:(I)轴建立空间直角坐标系,设出点的坐标,即可得到
=(2,-
,-
),
=(0,-3,-h),进而结合题意得到h=3.
(II)设平面A
1BC
1得法向量
=(a,b,c),根据题意求出
=(3,4,0),递减向量的射影进而求出点A到平面A
1BC
1的距离.
(III)设平面A
1BC的法向量为
=(x,y,z),由题意可得
=(0,1,-1),再利用向量之间的有关运算求出两个向量的夹角,进而转化为二面角的平面角得到答案.
解答:解:(I)分别以直线C
1B
1、CC
1、C
1A
1为x、y、z轴建立空间直角坐标系,
设|CA|=h,则C
1(0,0,0),B
1(4,0,0),B(4,-3,0),C(0,-3,0),A
1(0,0,h),A(0,-3,h),G(2,-
,-
)
∴
=(2,-
,-
),
=(0,-3,-h)
∴
•
=0,
∴h=3
(II)设平面A
1BC
1得法向量
=(a,b,c),
由题意可得:
=(0,0,3),
=(4,-3,0)所以
,即
,
则取
=(3,4,0),
∴点A到平面A
1BC
1的距离为h=|
|=
…(8分)
(III)设平面A
1BC的法向量为
=(x,y,z),
由题意可得:
=(4,0,0),
=(0,3,3),
所以
,即
,
则可求得
=(0,1,-1),
∴二面角C
1-A
1B-C的大小θ满足cosθ=
=
∴二面角C
1-A
1B-C的大小为arccos
点评:本题考查的知识点是二面角的平面角及求法,点到面的距离,以及求线段的长度问题,其中建立适当的空间坐标系,将问题转化为向量夹角及向量长度问题是解答本题的关键.

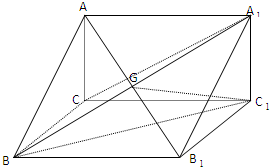 已知直三棱柱ABC-A1B1C1中,∠ACB=90°,CC1=3,BC=4,G是AB1和A1B的交点,若C1G⊥A1C.
已知直三棱柱ABC-A1B1C1中,∠ACB=90°,CC1=3,BC=4,G是AB1和A1B的交点,若C1G⊥A1C.

 学业测评一课一测系列答案
学业测评一课一测系列答案 如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CC1、AB中点.
如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CC1、AB中点.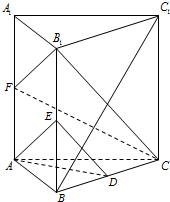 已知直三棱柱ABC-A1B1C1的所有棱长都相等,且D,E,F分别为BC,BB1,AA1的中点.
已知直三棱柱ABC-A1B1C1的所有棱长都相等,且D,E,F分别为BC,BB1,AA1的中点. 如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点,
如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点, 如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点.
如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点. 如图,已知直三棱柱ABC-A1B1C1中,AB=AC;M.N.P分别是棱BC.CC1.B1C1的中点.A1Q=3QA, BC=
如图,已知直三棱柱ABC-A1B1C1中,AB=AC;M.N.P分别是棱BC.CC1.B1C1的中点.A1Q=3QA, BC=