
【题目】已知函数![]() ,
,![]() .
.
![]() 当
当![]() 时,
时,![]() ,求实数a的取值范围;
,求实数a的取值范围;
![]() 当
当![]() 时,曲线
时,曲线![]() 和曲线
和曲线![]() 是否存在公共切线?并说明理由.
是否存在公共切线?并说明理由.
【答案】(1)![]() ;(2)存在公共切线,理由详见解析.
;(2)存在公共切线,理由详见解析.
【解析】
(1)构造函数![]() ,求出其最大值,解不等式即可得到实数
,求出其最大值,解不等式即可得到实数![]() 的取值范围;
的取值范围;
(2)假设存在这样的直线![]() 且直线
且直线![]() 与曲线和曲线
与曲线和曲线![]() 分别相切与点
分别相切与点![]() .分别求出两条切线方程,根据斜率与纵截距建立方程组,减元后得到
.分别求出两条切线方程,根据斜率与纵截距建立方程组,减元后得到![]() ,构造新函数研究单调性与极值即可.
,构造新函数研究单调性与极值即可.
解:![]() 令
令![]() ,则
,则![]() .
.
若![]() ,则
,则![]() ,若
,若![]() ,则
,则![]() .
.
所以![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数.
上是减函数.
所以![]() 是
是![]() 的极大值点,也是
的极大值点,也是![]() 的最大值点,即
的最大值点,即![]() .
.
若![]() 恒成立,则只需
恒成立,则只需![]() ,解得
,解得![]() .
.
所以实数![]() 的取值范围是
的取值范围是![]() .
.
![]() 假设存在这样的直线
假设存在这样的直线![]() 且与曲线
且与曲线![]() 和曲线
和曲线![]() 分别相切与点
分别相切与点![]() .
.
由![]() ,得
,得![]() .
.
曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]() .
.
同理可得,
曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]() .
.
所以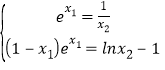 则
则![]() ,即
,即![]()
构造函数![]()
![]()
存在直线![]() 与曲线
与曲线![]() 和曲线
和曲线![]() 相切,
相切,
等价于函数![]() 在
在![]() 上有零点
上有零点
对于![]() .
.
当![]() 时,
时,![]() ,
,![]() 在上单调递增.
在上单调递增.
当![]() 时,因为
时,因为![]() ,所以
,所以![]() 在
在![]() 上是减函数.
上是减函数.
又![]() ,,所以存在
,,所以存在![]() ,使得
,使得![]() ,即
,即![]() .
.
且当![]() ,
,![]() 时,当
时,当![]() 时,
时,![]() .
.
综上,![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数.
上是减函数.
所以![]() 是
是![]() 的极大值,也是最大值,且
的极大值,也是最大值,且![]() .
.
又![]() ,
,![]() ,所以
,所以![]() 在
在![]() 内和
内和![]() 内各有一个零点.
内各有一个零点.
故假设成立,即曲线![]() 和曲线
和曲线![]() 存在公共切线.
存在公共切线.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面ABCD,底部ABCD为菱形,E为CD的中点.
平面ABCD,底部ABCD为菱形,E为CD的中点.

(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)若∠ABC=60°,求证:平面PAB⊥平面PAE;
(Ⅲ)棱PB上是否存在点F,使得CF∥平面PAE?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的离心率为
的离心率为![]() ,焦点为
,焦点为![]() 、
、![]() ,直线
,直线![]() 经过焦点
经过焦点![]() ,并与
,并与![]() 相交于
相交于![]() 、
、![]() 两点.
两点.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)在![]() 上是否存在
上是否存在![]() 、
、![]() 两点,满足
两点,满足![]() //
//![]() ,
,![]() ?若存在,求直线
?若存在,求直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设顶点在原点,焦点在![]() 轴上的拋物线过点
轴上的拋物线过点![]() ,过
,过![]() 作抛物线的动弦
作抛物线的动弦![]() ,
, ![]() ,并设它们的斜率分别为
,并设它们的斜率分别为![]() ,
, ![]() .
.
(Ⅰ)求拋物线的方程;
(Ⅱ)若![]() ,求证:直线
,求证:直线![]() 的斜率为定值,并求出其值;
的斜率为定值,并求出其值;
(III)若![]() ,求证:直线
,求证:直线![]() 恒过定点,并求出其坐标.
恒过定点,并求出其坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小学举办“父母养育我,我报父母恩”的活动,对六个年级(一年级到六年级的年级代码分别为1,2…,6)的学生给父母洗脚的百分比y%进行了调查统计,绘制得到下面的散点图.
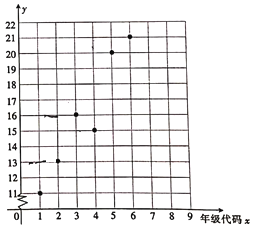
(1)由散点图看出,可用线性回归模型拟合y与x的关系,请用相关系数加以说明;
(2)建立y关于x的回归方程,并据此预计该校学生升入中学的第一年(年级代码为7)给父母洗脚的百分比.
附注:参考数据:![]()
参考公式:相关系数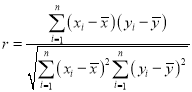 ,若r>0.95,则y与x的线性相关程度相当高,可用线性回归模型拟合y与x的关系.回归方程
,若r>0.95,则y与x的线性相关程度相当高,可用线性回归模型拟合y与x的关系.回归方程![]() 中斜率与截距的最小二乘估计公式分别为
中斜率与截距的最小二乘估计公式分别为![]() =
=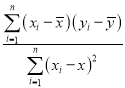 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1:![]() x2=1(a>1)与抛物线C2:x2=4y有相同焦点F1.
x2=1(a>1)与抛物线C2:x2=4y有相同焦点F1.
(1)求椭圆C1的标准方程;
(2)已知直线l1过椭圆C1的另一焦点F2,且与抛物线C2相切于第一象限的点A,设平行l1的直线l交椭圆C1于B,C两点,当△OBC面积最大时,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com