
【题目】如图,在四棱锥![]() 中,
中,![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,
,![]() .
.

(Ⅰ)在线段![]() 上找一点
上找一点![]() ,使得
,使得![]() 平面
平面![]() ,并证明你的结论;
,并证明你的结论;
(Ⅱ)若![]() ,
,![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】
(I)取线段![]() 上靠近
上靠近![]() 的三等分点
的三等分点![]() ,连接
,连接![]() ,因为
,因为![]() ,
,![]() ,所以
,所以![]() ,由
,由![]() ,得
,得![]() ,所以
,所以![]() ,即可证明结论成立.
,即可证明结论成立.
(II)以![]() 为坐标原点,以直线
为坐标原点,以直线![]() 分别为
分别为![]() 轴,过点
轴,过点![]() 且与
且与![]() 平面垂直的直线为
平面垂直的直线为![]() 轴建立空间直角坐标系,求出平面
轴建立空间直角坐标系,求出平面![]() 的一个法向量为
的一个法向量为![]() ,平面
,平面![]() 的个法向量为
的个法向量为![]() ,由向量法即可求出二面角的平面角.
,由向量法即可求出二面角的平面角.
(I)取线段![]() 上靠近
上靠近![]() 的三等分点
的三等分点![]() ,连接
,连接![]() .因为
.因为![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() .而
.而![]() ,所以
,所以![]() ,所以
,所以![]() .而
.而![]() 平面
平面![]() .
.![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() .
.
(II)易知 ![]()
![]() 为等边三角形,所以
为等边三角形,所以![]() .又
.又![]() ,故
,故![]() ,所以有
,所以有![]() .由已知可得
.由已知可得![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() .以
.以![]() 为坐标原点,以直线
为坐标原点,以直线![]() 分别为
分别为![]() 轴,过点
轴,过点![]() 且与
且与![]() 平面垂直的直线为
平面垂直的直线为![]() 轴建立如图所示的空间直角坐标系.
轴建立如图所示的空间直角坐标系.
设![]() ,则
,则![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,则有
,则有 即
即
设![]() ,则
,则![]() ,所以
,所以![]() .
.
设平面![]() 的个法向量为
的个法向量为![]() ,则有
,则有 即
即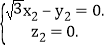
令![]() ,则
,则![]() ,所以
,所以![]() .
.
所以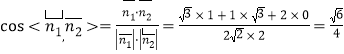 .
.
因为二面角![]() 为锐角,故所求二面角的余弦值为
为锐角,故所求二面角的余弦值为![]() .
.



 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
【题目】
一个盒子中装有4张卡片,每张卡片上写有1个数字,数字分别是1、2、3、4.现从盒子中随机抽取卡片.
(1)若一次抽取3张卡片,求3张卡片上数字之和大于7的概率;
(2)若第一次抽1张卡片,放回后再抽取1张卡片,求两次抽取中至少一次抽到数字3的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},从中选取第i1项、第i2项、…、第im项(i1<i2<…<im),若![]() ,则称新数列
,则称新数列![]() 为{an}的长度为m的递增子列.规定:数列{an}的任意一项都是{an}的长度为1的递增子列.
为{an}的长度为m的递增子列.规定:数列{an}的任意一项都是{an}的长度为1的递增子列.
(Ⅰ)写出数列1,8,3,7,5,6,9的一个长度为4的递增子列;
(Ⅱ)已知数列{an}的长度为p的递增子列的末项的最小值为![]() ,长度为q的递增子列的末项的最小值为
,长度为q的递增子列的末项的最小值为![]() .若p<q,求证:
.若p<q,求证:![]() <
<![]() ;
;
(Ⅲ)设无穷数列{an}的各项均为正整数,且任意两项均不相等.若{an}的长度为s的递增子列末项的最小值为2s–1,且长度为s末项为2s–1的递增子列恰有2s-1个(s=1,2,…),求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国道路交通安全法》第47条的相关规定:机动车行经人行道时,应当减速慢行;遇行人正在通过人行道,应当停车让行,俗称“礼让斑马线”, 《中华人民共和国道路交通安全法》第90条规定:对不礼让行人的驾驶员处以扣3分,罚款50元的处罚.下表是某市一主干路口监控设备所抓拍的5个月内驾驶员“礼让斑马线”行为统计数据:
月份 | 1 | 2 | 3 | 4 | 5 |
违章驾驶员人数 | 120 | 105 | 100 | 90 | 85 |
(1)请利用所给数据求违章人数![]() 与月份
与月份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(2)预测该路口9月份的不“礼让斑马线”违章驾驶员人数.
参考公式:  ,
, ![]() .
.
参考数据: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线E:y2=2px(p>0)的准线为l,圆C:(x﹣![]() )2+y2=4,l与圆C交于A,B,圆C与E交于M,N.若A,B,M,N为同一个矩形的四个顶点,则E的方程为( )
)2+y2=4,l与圆C交于A,B,圆C与E交于M,N.若A,B,M,N为同一个矩形的四个顶点,则E的方程为( )
A. y2=xB. y2=![]() xC. y2=2xD. y2=2
xC. y2=2xD. y2=2![]() x
x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某校组织的高二女子排球比赛中,有![]() 、
、![]() 两个球队进入决赛,决赛采用7局4胜制.假设
两个球队进入决赛,决赛采用7局4胜制.假设![]() 、
、![]() 两队在每场比赛中获胜的概率都是
两队在每场比赛中获胜的概率都是![]() .并记需要比赛的场数为
.并记需要比赛的场数为![]() .
.
(Ⅰ)求![]() 大于4的概率;
大于4的概率;
(Ⅱ)求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com