
【题目】设函数![]() 定义域为
定义域为![]() ,如果存在非实数
,如果存在非实数![]() 对任意的
对任意的![]() 都有
都有![]() ,则称函数
,则称函数![]() 是“似周期函数”,非零常数
是“似周期函数”,非零常数![]() 为函数
为函数![]() 的似周期.现有下列四个关于“似周期函数”的命题:
的似周期.现有下列四个关于“似周期函数”的命题:
①如果“似周期函数”![]() 的“似周期”为
的“似周期”为![]() ,那么它是周期为
,那么它是周期为![]() 的周期函数;
的周期函数;
②函数![]() 是“似周期函数”;
是“似周期函数”;
③函数![]() 是“似周期函数”;
是“似周期函数”;
④如果函数![]() 是“似周期函数”.那么”
是“似周期函数”.那么”![]()
其中是真命题的序号是____.(请填写所有满足条件的命题序号)
 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:
【题目】设(x1 , y1),(x2 , y2),…,(xn , yn),是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归方程(如图),以下结论中正确的是( ) 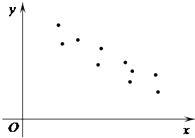
A.x和y正相关
B.x和y的相关系数为直线l的斜率
C.x和y的相关系数在﹣1到0之间
D.当n为偶数时,分布在l两侧的样本点的个数一定相同
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为![]() ,现有甲,乙二人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,……,取后不放回,直到两人中有一人取到白球即终止,每个球在每一次被取出的机会是等可能的.
,现有甲,乙二人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,……,取后不放回,直到两人中有一人取到白球即终止,每个球在每一次被取出的机会是等可能的.
(Ⅰ)求袋中原有白球的个数:
(Ⅱ)求取球次数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究学生的数学核素养与抽象(能力指标![]() )、推理(能力指标
)、推理(能力指标![]() )、建模(能力指标
)、建模(能力指标![]() )的相关性,并将它们各自量化为1、2、3三个等级,再用综合指标
)的相关性,并将它们各自量化为1、2、3三个等级,再用综合指标![]() 的值评定学生的数学核心素养;若
的值评定学生的数学核心素养;若![]() ,则数学核心素养为一级;若
,则数学核心素养为一级;若![]() ,则数学核心素养为二级;若
,则数学核心素养为二级;若![]() ,则数学核心素养为三级,为了了解某校学生的数学核素养,调查人员随机访问了某校10名学生,得到如下结果:
,则数学核心素养为三级,为了了解某校学生的数学核素养,调查人员随机访问了某校10名学生,得到如下结果:
学生编号 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)在这10名学生中任取两人,求这两人的建模能力指标相同的概率;
(2)从数学核心素养等级是一级的学生中任取一人,其综合指标为![]() ,从数学核心素养等级不是一级的学生中任取一人,其综合指标为
,从数学核心素养等级不是一级的学生中任取一人,其综合指标为![]() ,记随机变量
,记随机变量![]() ,求随机变量
,求随机变量![]() 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知(2x-3y)9=a0x9+a1x8y+a2x7y2+…+a9y9,求:
(1)各项系数之和;
(2)所有奇数项系数之和;
(3)系数绝对值的和;
(4)分别求出奇数项的二项式系数之和与偶数项的二项式系数之和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)函数![]() 在区间
在区间![]() 是单调函数,求实数
是单调函数,求实数![]() 的取值范围;
的取值范围;
(2)若存在![]() ,使得
,使得![]() 成立,求满足条件的最大整数
成立,求满足条件的最大整数![]() ;
;
(3)如果对任意的![]() 都有
都有![]() 成立,求实数
成立,求实数![]() 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】8人排成一排照相,分别求下列条件下的不同照相方式的种数.
(1)其中甲、乙相邻,丙、丁相邻;
(2)其中甲、乙不相邻,丙、丁不相邻;
(要求写出解答过程,并用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两定点![]() ,
, ![]() 和一动点
和一动点![]() ,给出下列结论:
,给出下列结论:
①若![]() ,则点
,则点![]() 的轨迹是椭圆;
的轨迹是椭圆;
②若![]() ,则点
,则点![]() 的轨迹是双曲线;
的轨迹是双曲线;
③若![]() ,则点
,则点![]() 的轨迹是圆;
的轨迹是圆;
④若![]() ,则点
,则点![]() 的轨迹关于原点对称;
的轨迹关于原点对称;
⑤若直线![]() 与
与![]() 斜率之积等于
斜率之积等于![]() ,则点
,则点![]() 的轨迹是椭圆(除长轴两端点).
的轨迹是椭圆(除长轴两端点).
其中正确的是__________(填序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com