
【题目】已知(2x-3y)9=a0x9+a1x8y+a2x7y2+…+a9y9,求:
(1)各项系数之和;
(2)所有奇数项系数之和;
(3)系数绝对值的和;
(4)分别求出奇数项的二项式系数之和与偶数项的二项式系数之和.
【答案】(1)-1;(2)![]() ;(3)59;(4)28.
;(3)59;(4)28.
【解析】试题分析:(1)令x=1,y=1进行赋值即可;(2)令x=1,y=-1赋值结合(1)即可求出;(3)去掉绝对值号求即可;(4)根据性质各等二项式系数和的一半.
试题解析:(1)令x=1,y=1,得
a0+a1+a2+…+a9=(2-3)9=-1.
(2)由(1)知,a0+a1+a2+…+a9=-1.
令x=1,y=-1,可得a0-a1+a2-…-a9=59.
将两式相加,可得a0+a2+a4+a6+a8=![]() .
.
(3)法一:|a0|+|a1|+|a2|+…+|a9|=a0-a1+a2-a3+…-a9,
令x=1,y=-1,则|a0|+|a1|+|a2|+…+|a9|=a0-a1+a2-a3+…-a9=59.
法二:|a0|+|a1|+|a2|+…+|a9|即为(2x+3y)9的展开式中各项的系数和,令x=1,y=1,得
|a0|+|a1|+|a2|+…+|a9|=59.
(4)奇数项的二项式系数之和为
C+C+…+C=28.
偶数项的二项式系数之和为C+C+…+C=28.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C的对边分别为a,b,c.角A,B,C成等差数列.
(1)求cosB的值;
(2)边a,b,c成等比数列,求sinAsinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,0<φ< ![]() )图象如图,P是图象的最高点,Q为图象与x轴的交点,O为原点.且|OQ|=2,|OP|=
)图象如图,P是图象的最高点,Q为图象与x轴的交点,O为原点.且|OQ|=2,|OP|= ![]() ,|PQ|=
,|PQ|= ![]() .
. 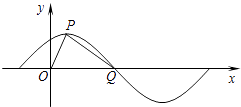
(1)求函数y=f(x)的解析式;
(2)将函数y=f(x)图象向右平移1个单位后得到函数y=g(x)的图象,当x∈[0,2]时,求函数h(x)=f(x)g(x)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2 ![]() ,四边形BDEF是平行四边形,BD与AC交于点G,O为GC的中点,且FO⊥平面ABCD,FO=
,四边形BDEF是平行四边形,BD与AC交于点G,O为GC的中点,且FO⊥平面ABCD,FO= ![]() .
. 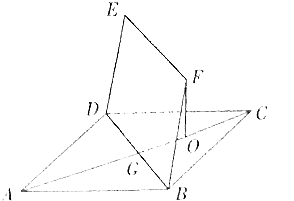
(1)求BF与平面ABCD所成的角的正切值;
(2)求三棱锥O﹣ADE的体积;
(3)求证:平面AEF⊥平面BCF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 定义域为
定义域为![]() ,如果存在非实数
,如果存在非实数![]() 对任意的
对任意的![]() 都有
都有![]() ,则称函数
,则称函数![]() 是“似周期函数”,非零常数
是“似周期函数”,非零常数![]() 为函数
为函数![]() 的似周期.现有下列四个关于“似周期函数”的命题:
的似周期.现有下列四个关于“似周期函数”的命题:
①如果“似周期函数”![]() 的“似周期”为
的“似周期”为![]() ,那么它是周期为
,那么它是周期为![]() 的周期函数;
的周期函数;
②函数![]() 是“似周期函数”;
是“似周期函数”;
③函数![]() 是“似周期函数”;
是“似周期函数”;
④如果函数![]() 是“似周期函数”.那么”
是“似周期函数”.那么”![]()
其中是真命题的序号是____.(请填写所有满足条件的命题序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为![]() =0.85x-85.71,则下列结论中不正确的是( )
=0.85x-85.71,则下列结论中不正确的是( )
A. y与x具有正的线性相关关系
B. 若给变量x一个值,由回归直线方程![]() =0.85x-85.71得到一个
=0.85x-85.71得到一个![]() ,则
,则![]() 为该统计量中的估计值
为该统计量中的估计值
C. 若该大学某女生身高增加1 cm,则其体重约增加0.85 kg
D. 若该大学某女生身高为170 cm,则可断定其体重必为58.79 kg
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得 =80, =20, i=184, =720.
(1)求家庭的月储蓄y对月收入x的线性回归方程![]() ;
;
(2)判断变量x与y之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:线性回归方程![]() 中,
中, ![]() ,其中
,其中![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,圆心为
,圆心为![]() ,定点
,定点![]() ,
, ![]() 为圆
为圆![]() 上一点,线段
上一点,线段![]() 上一点
上一点![]() 满足
满足![]() ,直线
,直线![]() 上一点
上一点![]() ,满足
,满足![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)![]() 为坐标原点,
为坐标原点, ![]() 是以
是以![]() 为直径的圆,直线
为直径的圆,直线![]() 与
与![]() 相切,并与轨迹
相切,并与轨迹![]() 交于不同的两点
交于不同的两点![]() .当
.当![]() 且满足
且满足![]() 时,求
时,求![]() 面积
面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com