
【题目】设函数![]() .
.
(1)函数![]() 在区间
在区间![]() 是单调函数,求实数
是单调函数,求实数![]() 的取值范围;
的取值范围;
(2)若存在![]() ,使得
,使得![]() 成立,求满足条件的最大整数
成立,求满足条件的最大整数![]() ;
;
(3)如果对任意的![]() 都有
都有![]() 成立,求实数
成立,求实数![]() 的范围.
的范围.
【答案】(1)![]() ; (2)最大正整数
; (2)最大正整数![]() ;(3)
;(3) ![]() .
.
【解析】试题分析:(1)分析条件可得![]() ,在区间
,在区间![]() 上恒成立,只需
上恒成立,只需![]() 即可;
即可;
(2)存在![]() ,使得
,使得![]() 成立,等价于
成立,等价于![]() ,考察
,考察![]() ,从而化为求g(x)的最值,从而求解;
,从而化为求g(x)的最值,从而求解;
(3)化简可知![]() 的最大值是1,从而可得只需当
的最大值是1,从而可得只需当![]() 时,
时,![]() 恒成立,等价于
恒成立,等价于![]() 恒成立,从而转化为函数最值问题.
恒成立,从而转化为函数最值问题.
试题解析:
(1)![]() ,定义域为
,定义域为![]() ,函数
,函数![]() 在
在![]() 上是单调函数,
上是单调函数,
即![]() ,在区间
,在区间![]() 上恒成立.
上恒成立.
亦即![]() 在区间
在区间![]() 上恒成立,显然有
上恒成立,显然有![]() .
.
(2)存在![]() ,使得
,使得![]() 成立,等价于
成立,等价于![]() ,考察
,考察![]() .
.
|
|
|
|
|
|
| 3 |
| + |
| - |
| + | ||
|
| 递增 | -3 | 递减 |
| 递增 | 15 |
由表可知![]() ,
,![]() .
.
![]() ,所以满足条件的最大正整数
,所以满足条件的最大正整数![]() .
.
(3)当![]() 时,由(2)可知,
时,由(2)可知,![]() 先减后增,而
先减后增,而![]() ,所以
,所以![]() 的最大值是
的最大值是![]() .要满足条件,则只需当
.要满足条件,则只需当![]() 时,
时,![]() 恒成立,等价于
恒成立,等价于![]() 恒成立.
恒成立.
记![]() 当
当![]() 时,
时,![]() ,即函数
,即函数![]() 在区间
在区间![]() 上递增.
上递增.
当![]() 时
时![]() ,即函数
,即函数![]() 在区间
在区间![]() 上递减.
上递减.
所以![]() ,所以
,所以![]() .
.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:
【题目】参加市数学调研抽测的某校高三学生成绩分析的茎叶图和频率分布直方图均受到不同程度的破坏,但可见部分信息如下,据此解答如下问题: 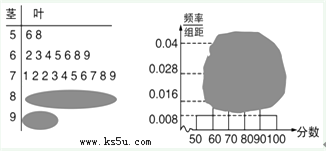
(1)求参加数学抽测的人数n、抽测成绩的中位数及分数分别在[80,90),[90,100]内的人数;
(2)若从分数在[80,100]内的学生中任选两人进行调研谈话,求恰好有一人分数在[90,100]内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率是
的离心率是![]() ,且过点
,且过点![]() .直线
.直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)求![]() 的面积的最大值;
的面积的最大值;
(Ⅲ)设直线![]() ,
, ![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
, ![]() .判断
.判断![]() ,
, ![]() 大小关系,并加以证明.
大小关系,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 定义域为
定义域为![]() ,如果存在非实数
,如果存在非实数![]() 对任意的
对任意的![]() 都有
都有![]() ,则称函数
,则称函数![]() 是“似周期函数”,非零常数
是“似周期函数”,非零常数![]() 为函数
为函数![]() 的似周期.现有下列四个关于“似周期函数”的命题:
的似周期.现有下列四个关于“似周期函数”的命题:
①如果“似周期函数”![]() 的“似周期”为
的“似周期”为![]() ,那么它是周期为
,那么它是周期为![]() 的周期函数;
的周期函数;
②函数![]() 是“似周期函数”;
是“似周期函数”;
③函数![]() 是“似周期函数”;
是“似周期函数”;
④如果函数![]() 是“似周期函数”.那么”
是“似周期函数”.那么”![]()
其中是真命题的序号是____.(请填写所有满足条件的命题序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边长分别为a,b,c,B= ![]() .
.
(1)若a=3,b= ![]() ,求c的值;
,求c的值;
(2)若f(A)=sinA( ![]() cosA﹣sinA),a=
cosA﹣sinA),a= ![]() ,求f(A)的最大值及此时△ABC的外接圆半径.
,求f(A)的最大值及此时△ABC的外接圆半径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得 =80, =20, i=184, =720.
(1)求家庭的月储蓄y对月收入x的线性回归方程![]() ;
;
(2)判断变量x与y之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:线性回归方程![]() 中,
中, ![]() ,其中
,其中![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:在数列![]() 中,若
中,若![]() 为常数)则称
为常数)则称![]() 为“等方差数列”,下列是对“等方差数列”的有关判断( )
为“等方差数列”,下列是对“等方差数列”的有关判断( )
①若![]() 是“等方差数列”,在数列
是“等方差数列”,在数列![]() 是等差数列;
是等差数列;
②![]() 是“等方差数列”;
是“等方差数列”;
③若![]() 是“等方差数列”,则数列
是“等方差数列”,则数列![]() 为常)也是“等方差数列”;
为常)也是“等方差数列”;
④若![]() 既是“等方差数列”又是等差数列,则该数列是常数数列.
既是“等方差数列”又是等差数列,则该数列是常数数列.
其中正确命题的个数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com