
分析 化简g(x),求出f(x),g(x)在[1,4]上的值域,令两值域有公共解即可.
解答 解:f(x)的图象开口向下,对称轴为x=2,
∴f(x)在[1,4]上的最大值为f(2)=1,最小值为f(4)=-3.
∴f(x)的值域为[-3,1],
g(x)=2sin($\frac{π}{6}x$)[$\frac{1}{2}$sin($\frac{π}{6}$x)+$\frac{\sqrt{3}}{2}$cos$\frac{π}{6}x$]+a=sin2($\frac{π}{6}x$)+$\sqrt{3}$sin($\frac{π}{6}x$)cos($\frac{π}{6}x$)+a
=$\frac{1-cos(\frac{π}{3}x)}{2}$+$\frac{\sqrt{3}}{2}$sin$\frac{π}{3}x$+a=sin($\frac{π}{3}$x-$\frac{π}{6}$)+$\frac{1}{2}$+a,
∵x∈[1,4],∴$\frac{π}{3}$x-$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{7π}{6}$],
∴a≤g(x)≤$\frac{3}{2}$+a,即g(x)的值域为[a,a+$\frac{3}{2}$].
∵存在x1,x2∈[1,4],使得f(x1)=g(x2)成立,
∴[-3,1]∩[a,a+$\frac{3}{2}$]≠∅.
-3≤a≤1或-3≤a+$\frac{3}{2}$≤1,
解得-$\frac{9}{2}$≤a≤1.
故答案为[-$\frac{9}{2}$,1].
点评 本题考查了函数值域的求法,三角函数恒等变换,集合的关系,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
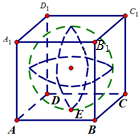 已知棱长为1的正方体有一个内切球(如图),E为ABCD的中心,A1E与球相交于FE,则EF的长为$\frac{{\sqrt{6}}}{3}$.
已知棱长为1的正方体有一个内切球(如图),E为ABCD的中心,A1E与球相交于FE,则EF的长为$\frac{{\sqrt{6}}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
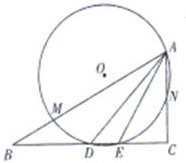 如图,已知在△ABC中,AE,AD分别为其角平分线和中线,△ADE的外接圆为⊙O,⊙O与AB,AC分别交于M,N,求证:
如图,已知在△ABC中,AE,AD分别为其角平分线和中线,△ADE的外接圆为⊙O,⊙O与AB,AC分别交于M,N,求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com