
【题目】如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°. 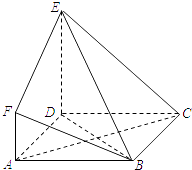
(1)求证:AC⊥平面BDE;
(2)设点M是线段BD上一个动点,试确定点M的位置,使得AM∥平面BEF,并证明你的结论.
【答案】
(1)证明:因为DE⊥平面ABCD,
所以DE⊥AC.
因为ABCD是正方形,
所以AC⊥BD,因为DE∩BD=D
从而AC⊥平面BDE.
(2)解:当M是BD的一个三等分点,即3BM=BD时,AM∥平面BEF.
取BE上的三等分点N,使3BN=BE,连接MN,NF,则DE∥MN,且DE=3MN,
因为AF∥DE,且DE=3AF,所以AF∥MN,且AF=MN,
故四边形AMNF是平行四边形.
所以AM∥FN,
因为AM平面BEF,FN平面BEF,
所以AM∥平面BEF.
【解析】(1)根据DE⊥平面ABCD,由线面垂直的判定定理可知DE⊥AC,由ABCD是正方形可知AC⊥BD,而DE∩BD=D,满足线面垂直的判定所需条件,从而证得结论;(2)当M是BD的一个三等分点,即3BM=BD时,AM∥平面BEF.取BE上的三等分点N,使3BN=BE,连接MN,NF,则DE∥MN,且DE=3MN,而AF∥DE,且DE=3AF,则四边形AMNF是平行四边形,从而AM∥FN,AM平面BEF,FN平面BEF,满足线面平行的判定定理,从而证得结论.
【考点精析】本题主要考查了直线与平面平行的判定和直线与平面垂直的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱![]() 中,底面
中,底面![]() 是边长为2的正方形,
是边长为2的正方形, ![]() 分别为线段
分别为线段![]() ,
, ![]() 的中点.
的中点.

(1)求证: ![]() ||平面
||平面![]() ;
;
(2)四棱柱![]() 的外接球的表面积为
的外接球的表面积为![]() ,求异面直线
,求异面直线![]() 与
与![]() 所成的角的大小.
所成的角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
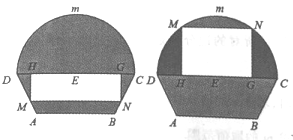
【题目】如图所示的自动通风设施.该设施的下部![]() 是等腰梯形,其中
是等腰梯形,其中![]() 为2米,梯形的高为1米,
为2米,梯形的高为1米, ![]() 为3米,上部
为3米,上部![]() 是个半圆,固定点
是个半圆,固定点![]() 为
为![]() 的中点.
的中点. ![]() 是由电脑控制可以上下滑动的伸缩横杆(横杆面积可忽略不计),且滑动过程中始终保持和
是由电脑控制可以上下滑动的伸缩横杆(横杆面积可忽略不计),且滑动过程中始终保持和![]() 平行.当
平行.当![]() 位于
位于![]() 下方和上方时,通风窗的形状均为矩形
下方和上方时,通风窗的形状均为矩形![]() (阴影部分均不通风).
(阴影部分均不通风).
(1)设![]() 与
与![]() 之间的距离为
之间的距离为![]() (
(![]() 且
且![]() )米,试将通风窗的通风面积
)米,试将通风窗的通风面积![]() (平方米)表示成关于
(平方米)表示成关于![]() 的函数
的函数![]() ;
;
(2)当![]() 与
与![]() 之间的距离为多少米时,通风窗的通风面积
之间的距离为多少米时,通风窗的通风面积![]() 取得最大值?
取得最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的前n项和为Sn , 且满足4Sn﹣1=an2+2an , n∈N* .
(1)求数列{an}的通项公式;
(2)设bn= ![]() ,数列{bn}的前n项和为Tn , 证明:
,数列{bn}的前n项和为Tn , 证明: ![]() ≤Tn<
≤Tn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学名著,也是古代东方数学的代表作.书中有如下问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“已知直角三角形两直角边长分别为5步和12步,问其内接正方形边长为多少步?”现若向此三角形内投豆子,则落在其内接正方形内的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(
=( ![]() sin3x,﹣y),
sin3x,﹣y), ![]() =(m,cos3x﹣m)(m∈R),且
=(m,cos3x﹣m)(m∈R),且 ![]() +
+ ![]() =
= ![]() .设y=f(x).
.设y=f(x).
(1)求f(x)的表达式,并求函数f(x)在[ ![]() ,
, ![]() ]上图象最低点M的坐标.
]上图象最低点M的坐标.
(2)在△ABC中,f(A)=﹣ ![]() ,且A>
,且A> ![]() π,D为边BC上一点,AC=
π,D为边BC上一点,AC= ![]() DC,BD=2DC,且AD=2
DC,BD=2DC,且AD=2 ![]() ,求线段DC的长.
,求线段DC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“六一”联欢会上设有一个抽奖游戏.抽奖箱中共有12张纸条,分一等奖、二等奖、三等奖、无奖四种.从中任取一张,不中奖的概率为![]() ,中二等奖或三等奖的概率是
,中二等奖或三等奖的概率是![]() .
.
(Ⅰ)求任取一张,中一等奖的概率;
(Ⅱ)若中一等奖或二等奖的概率是![]() ,求任取一张,中三等奖的概率.
,求任取一张,中三等奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,BC边上的高AM所在的直线方程为x-2y+1=0,∠A的平分线所在的直线方程为y=0与BC相交于点P,若点B的坐标为(1,2).

(1)分别求AB和BC所在直线的方程;
(2)求P点坐标和AC所在直线的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com