
【题目】如图,在△ABC中,BC边上的高AM所在的直线方程为x-2y+1=0,∠A的平分线所在的直线方程为y=0与BC相交于点P,若点B的坐标为(1,2).

(1)分别求AB和BC所在直线的方程;
(2)求P点坐标和AC所在直线的方程.
科目:高中数学 来源: 题型:
【题目】若关于x的方程x2﹣(a2+b2﹣6b)x+a2+b2+2a﹣4b+1=0的两个实数根x1 , x2满足x1≤0≤x2≤1,则a2+b2+4a的最小值和最大值分别为( )
A.![]() 和5+4
和5+4 ![]()
B.﹣ ![]() 和5+4
和5+4 ![]()
C.﹣ ![]() 和12
和12
D.﹣ ![]() 和15﹣4
和15﹣4 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°. 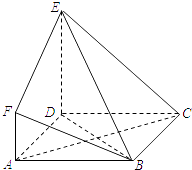
(1)求证:AC⊥平面BDE;
(2)设点M是线段BD上一个动点,试确定点M的位置,使得AM∥平面BEF,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx+1(a,b为实数),设![]() ,
,
(1)若f(-1)=0,且对任意实数x均有f(x)≥0成立,求F(x)的表达式;
(2)在(1)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围;
(3)设mn<0,m+n>0,a>0,且f(x)满足f(-x)=f(x),试比较F(m)+F(n)的值与0的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点![]() ,焦点在
,焦点在![]() 轴上,离心率为
轴上,离心率为![]() 的椭圆过点
的椭圆过点 .
.
(1)求椭圆的方程;
(2)设不过原点![]() 的直线
的直线![]() 与该椭圆交于
与该椭圆交于![]() 两点,满足直线
两点,满足直线![]() 的斜率依次成等比数列,求
的斜率依次成等比数列,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AB∥C,AD=DC=CB=1,∠ABC═60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1. 
(1)求证:BC⊥平面ACFE;
(2)求二面角A﹣BF﹣C的平面角的余弦值;
(3)若点M在线段EF上运动,设平MAB与平FCB所成二面角的平面角为θ(θ≤90°),试求cosθ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年4月23日“世界读书日”来临之际,某校为了了解中学生课外阅读情况,随机抽取了100名学生,并获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表.
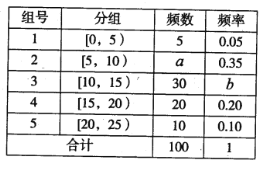
(Ⅰ)求![]() 的值,并作出这些数据的频率分布直方图;
的值,并作出这些数据的频率分布直方图;

(Ⅱ)假设每组数据组间是平均分布的,试估计该组数据的平均数;(同一组中的数据用该组区间的中点值作代表);
(Ⅲ)现从第3、4、5组中用分层抽样的方法抽取6人参加校“中华诗词比赛”,经过比赛后从这6人中选拔2人组成该校代表队,求这2人来自不同组别的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,AB⊥平面BCP,CD∥平面ABP,AB=BC=CP=BP=2CD=2 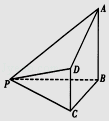
(1)证明:平面ABP⊥平面ADP;
(2)若直线PA与平面PCD所成角为α,求sinα的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com