
【题目】如图,在四棱锥![]() 中,直线
中,直线![]() 平面
平面![]() ,
,![]() .
.
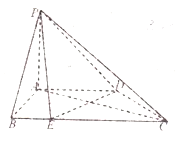
(1)求证:直线![]() 平面
平面![]() .
.
(2)若直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ,求二面角
,求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
【答案】(1)详见解析(2)![]()
【解析】
试题分析:(1)证明线面垂直,一般多次利用线面垂直判定定理及性质定理,经多次线线垂直与线面垂直的转化进行论证:在线线垂直论证与寻找时,要注意利用平面几何的条件,如本题就利用两三角形相似![]()
![]() ,得到
,得到![]() ,再根据线面垂直性质定理将条件
,再根据线面垂直性质定理将条件![]() 平面
平面![]() 转化为线线垂直:
转化为线线垂直:![]() ,最后根据线面垂直判定定理得
,最后根据线面垂直判定定理得![]() 平面
平面![]() (2)线面角找射影,由(1)知直线
(2)线面角找射影,由(1)知直线![]() 在平面
在平面![]() 上射影为
上射影为![]() (
(![]() 为
为![]() 与
与![]() 交点),则
交点),则![]() 是直线
是直线![]() 与平面
与平面![]() 所成的角,二面角的作法,往往结合三垂线定理:作
所成的角,二面角的作法,往往结合三垂线定理:作![]() 于
于![]() ,由
,由![]() ,知
,知![]() 平面
平面![]() ,∴
,∴![]() ,∴
,∴![]() 是二面角
是二面角![]() 的平面角,最后结合对应三角形求角的三角函数值.本题也可建立空间直角坐标系进行论证、求解.
的平面角,最后结合对应三角形求角的三角函数值.本题也可建立空间直角坐标系进行论证、求解.
试题解析:
法一:(1)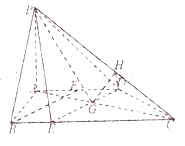
取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() ,
,
∴四边形![]() 是平行四边形,∴
是平行四边形,∴![]() .
.
∵直角![]() 和直角
和直角![]() 中,
中,![]() ,∴直角
,∴直角![]() 直角
直角![]() ,易知
,易知![]() ,
,
∴![]()
又∵![]() 平面
平面![]() ,∴
,∴![]()
而![]() ,∴
,∴![]() 平面
平面![]() ,得证
,得证
(2)由![]() ,知
,知![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
设![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,则
,则![]() 是直线
是直线![]() 与平面
与平面![]() 所成的角,
所成的角,
![]() ,∴
,∴![]() ,而
,而![]() 故
故![]()
作![]() 于
于![]() ,由
,由![]() ,知
,知![]() 平面
平面![]() ,∴
,∴![]() ,∴
,∴![]() 是二面角
是二面角![]() 的平面角
的平面角
∵![]() ,∴
,∴![]() ,而
,而![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() ,即二面角
,即二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]()
法二: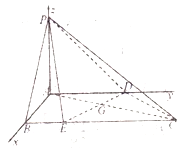
(1)∵![]() 平面
平面![]() ,∴
,∴![]() ,又∵
,又∵![]() ,故可建立如图所示坐标系
,故可建立如图所示坐标系
由已知![]() ,∴
,∴![]() ,∴
,∴![]()
![]()
∴![]() ,∴
,∴![]() 平面
平面![]()
(2)由(1),平面![]() 的一个法向量是
的一个法向量是![]() ,
,
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,∴
,∴![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() ,即
,即![]()
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由![]() ,∴
,∴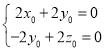 ,令
,令![]() ,则
,则![]()
∴![]()
显然二面角![]() 的平面角是锐角,
的平面角是锐角,
∴二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]()


科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的前n项和为Sn , 且满足4Sn﹣1=an2+2an , n∈N* .
(1)求数列{an}的通项公式;
(2)设bn= ![]() ,数列{bn}的前n项和为Tn , 证明:
,数列{bn}的前n项和为Tn , 证明: ![]() ≤Tn<
≤Tn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,BC边上的高AM所在的直线方程为x-2y+1=0,∠A的平分线所在的直线方程为y=0与BC相交于点P,若点B的坐标为(1,2).

(1)分别求AB和BC所在直线的方程;
(2)求P点坐标和AC所在直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() (k∈R).
(k∈R).
(1)求函数y=f(x)的单调区间;
(2)若k∈N*,且当x∈(1,+∞)时,f(x)>0恒成立,求k的最大值.( ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|,其中a>1
(1)当a=2时,求不等式f(x)≥4﹣|x﹣4|的解集;
(2)已知关于x的不等式|f(2x+a)﹣2f(x)|≤2的解集{x|1≤x≤2},求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x∈(﹣∞,0),2x>3x;命题q:x∈(0, ![]() ),sinx>x,则下列命题为真命题的是( )
),sinx>x,则下列命题为真命题的是( )
A.p∧q
B.(¬p)∨q
C.(¬p)∧q
D.p∧(¬q)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 甲、乙二人比赛,甲胜的概率为![]() ,则比赛5场,甲胜3场
,则比赛5场,甲胜3场
B. 某医院治疗一种疾病的治愈率为10%,前9个病人没有治愈,则第10个病人一定治愈
C. 随机试验的频率与概率相等
D. 天气预报中,预报明天降水概率为90%,是指降水的可能性是90%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次考试中,从甲乙两个班各抽取10名学生的数学成绩进行统计分析,两个班成绩的茎叶图如图所示.

(Ⅰ)求甲班的平均分;
(Ⅱ)从甲班和乙班成绩90![]() 100的学生中抽取两人,求至少含有甲班一名同学的概率.
100的学生中抽取两人,求至少含有甲班一名同学的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com