
【题目】已知函数 ![]() (k∈R).
(k∈R).
(1)求函数y=f(x)的单调区间;
(2)若k∈N*,且当x∈(1,+∞)时,f(x)>0恒成立,求k的最大值.( ![]() )
)
【答案】
(1)解:f′(x)= ![]() ﹣
﹣ ![]() =
= ![]() ,(x>0).
,(x>0).
①k≤0时,f′(x)>0,∴函数f(x)在(0,+∞)上单调递增.
②k>0时,f′(x)= ![]() .
.
△=(2﹣k)2﹣4=k(k﹣4)≤0时,解得0<k≤4,f′(x)≥0,∴函数f(x)在(0,+∞)上单调递增.
△=k(k﹣4)>0,k>0时,解得k>4.由x2+(2﹣k)x+1=0,解得x= ![]() ,
,
取x1= ![]() ,x2=
,x2= ![]() .0<x1<x2.
.0<x1<x2.
∴f′(x)= ![]() .令f′(x)>0,解得x>x2,0<x<x1,则函数f(x)在(0,x1),(x2,+∞)上单调递增;在(x1,x2)上单调递减.
.令f′(x)>0,解得x>x2,0<x<x1,则函数f(x)在(0,x1),(x2,+∞)上单调递增;在(x1,x2)上单调递减.
综上可得:k≤4,函数f(x)在(0,+∞)上单调递增.
k>4时,函数f(x)在(0,x1),(x2,+∞)上单调递增;在(x1,x2)上单调递减,其中x1= ![]() ,x2=
,x2= ![]() ,0<x1<x2.
,0<x1<x2.
(2)解:由(I)可得:k≤4,函数f(x)在(0,+∞)上单调递增.而f(1)=5﹣ ![]() ≥3,∴当x∈(1,+∞)时,f(x)>0恒成立,满足条件.
≥3,∴当x∈(1,+∞)时,f(x)>0恒成立,满足条件.
k>4时,函数f(x)在(0,x1),(x2,+∞)上单调递增;在(x1,x2)上单调递减,其中x1= ![]() ,x2=
,x2= ![]() ,0<x1<x2.
,0<x1<x2.
由于x1= ![]() <1<x2,若f(1)=5﹣
<1<x2,若f(1)=5﹣ ![]() ≥0,解得k≤10.
≥0,解得k≤10.
k>10时舍去.
4<k≤10时,必须f(x2)>0,
由 ![]() +(2﹣k)x2+1=0,可得kx2=
+(2﹣k)x2+1=0,可得kx2= ![]() +2x2+1,
+2x2+1,
∴f(x2)=5+lnx2﹣ ![]() =4﹣x2+lnx2>0,
=4﹣x2+lnx2>0,
k=10时,由 ![]() ﹣8x2+1=0,x2>1,解得x2=4+
﹣8x2+1=0,x2>1,解得x2=4+ ![]() .
.
f(x2)=4﹣(4+ ![]() )+ln(4+
)+ln(4+ ![]() )=ln(4+
)=ln(4+ ![]() )﹣
)﹣ ![]() <0,舍去.
<0,舍去.
同理可得:k=9不满足条件舍去.
k=8时,由 ![]() ﹣6x2+1=0,x2>1,解得x2=3+2
﹣6x2+1=0,x2>1,解得x2=3+2 ![]() .
.
f(x2)=4﹣(3+2 ![]() )+ln(3+2
)+ln(3+2 ![]() )≈1﹣2
)≈1﹣2 ![]() +1.76<0,舍去.
+1.76<0,舍去.
k=7时,由 ![]() ﹣5x2+1=0,x2>1,解得x2=
﹣5x2+1=0,x2>1,解得x2= ![]() ∈(4.75,4.8).
∈(4.75,4.8).
f(x2)=4﹣x2+lnx2>0,
综上可得:当x∈(1,+∞)时,f(x)>0恒成立,k的最大值为7.
【解析】(I)f′(x)= ![]() ﹣
﹣ ![]() =
= ![]() ,(x>0).①k≤0时,f′(x)>0,可得单调性.②k>0时,f′(x)=
,(x>0).①k≤0时,f′(x)>0,可得单调性.②k>0时,f′(x)= ![]() .△≤0时,解得0<k≤4,f′(x)≥0,可得函数f(x)在(0,+∞)上单调递增.△>0,解得k>4.由x2+(2﹣k)x+1=0,取x1=
.△≤0时,解得0<k≤4,f′(x)≥0,可得函数f(x)在(0,+∞)上单调递增.△>0,解得k>4.由x2+(2﹣k)x+1=0,取x1= ![]() ,x2=
,x2= ![]() .0<x1<x2 . f′(x)=
.0<x1<x2 . f′(x)= ![]() .即可得出单调性.(II)由(I)可得:k≤4,函数f(x)在(0,+∞)上单调递增.而f(1)=5﹣
.即可得出单调性.(II)由(I)可得:k≤4,函数f(x)在(0,+∞)上单调递增.而f(1)=5﹣ ![]() ≥3,当x∈(1,+∞)时,f(x)>0恒成立,满足条件.k>4时,函数f(x)在在(1,x2)上单调递减,(x2 , +∞)上单调递增;1<x2 . 若f(1)=5﹣
≥3,当x∈(1,+∞)时,f(x)>0恒成立,满足条件.k>4时,函数f(x)在在(1,x2)上单调递减,(x2 , +∞)上单调递增;1<x2 . 若f(1)=5﹣ ![]() ≥0,解得k≤10.k>10时舍去.4<k≤10时,必须f(x2)>0,经过验证即可得出.
≥0,解得k≤10.k>10时舍去.4<k≤10时,必须f(x2)>0,经过验证即可得出.
【考点精析】利用利用导数研究函数的单调性对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx+1(a,b为实数),设![]() ,
,
(1)若f(-1)=0,且对任意实数x均有f(x)≥0成立,求F(x)的表达式;
(2)在(1)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围;
(3)设mn<0,m+n>0,a>0,且f(x)满足f(-x)=f(x),试比较F(m)+F(n)的值与0的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AB∥C,AD=DC=CB=1,∠ABC═60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1. 
(1)求证:BC⊥平面ACFE;
(2)求二面角A﹣BF﹣C的平面角的余弦值;
(3)若点M在线段EF上运动,设平MAB与平FCB所成二面角的平面角为θ(θ≤90°),试求cosθ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年4月23日“世界读书日”来临之际,某校为了了解中学生课外阅读情况,随机抽取了100名学生,并获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表.
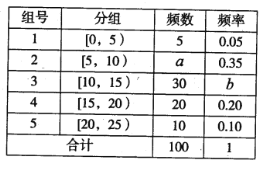
(Ⅰ)求![]() 的值,并作出这些数据的频率分布直方图;
的值,并作出这些数据的频率分布直方图;

(Ⅱ)假设每组数据组间是平均分布的,试估计该组数据的平均数;(同一组中的数据用该组区间的中点值作代表);
(Ⅲ)现从第3、4、5组中用分层抽样的方法抽取6人参加校“中华诗词比赛”,经过比赛后从这6人中选拔2人组成该校代表队,求这2人来自不同组别的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的参数方程为 ![]() (α为参数,α∈[0,π]),直线l的极坐标方程为
(α为参数,α∈[0,π]),直线l的极坐标方程为 ![]() .
.
(1)写出曲线C的普通方程和直线l的直角坐标方程;
(2)P为曲线C上任意一点,Q为直线l任意一点,求|PQ|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人都准备于下午12:00-13:00之间到某车站乘某路公交车外出,设在12:00-13:00之间有四班该路公交车开出,已知开车时间分别为12:20,12:30,12:40,13:00,分别求他们在下述情况下坐同一班车的概率.
(1)他们各自选择乘坐每一班车是等可能的;
(2)他们各自到达车站的时刻是等可能的(有车就乘).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com