Question

20．已知函数$\begin{array}{l}f（x）=\left\{\begin{array}{l}{e^x}-1，（{x＜1}）\\{x^3}-9{x^2}+24x-16，（{x≥1}）\end{array}\right.\end{array}$，则关于x的方程|f（x）|=a（a为实数）根个数不可能为（　　）

• A． 1
• B． 3
• C． 5
• D． 6

Answer 1

分析 判断f（x）的单调性，计算f（x）的极值，作出y=|f（x）|的函数图象，根据函数图象得出方程|f（x）|=a的解的情况．

解答 解：当x＜1时，f（x）为增函数，且f（0）=0，
当x≥1时，f′（x）=3x²-18x+24，
令f′（x）=0得3x²-18x+24=0，解得x₁=2，x₂=4，
当1≤x＜2时，f′（x）＞0，当2＜x＜4时，f′（x）＜0，当x＞4时，f′（x）＞0，
∴当x=2时，f（x）取得极大值f（2）=4，当x=4时，f（x）取得极小值f（4）=0，
做出y=f（x）的函数图象如图：

将x轴下方的图象向上翻折得出y=|f（x）|的函数图象如图所示：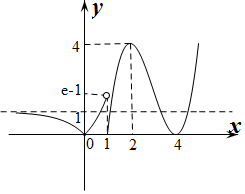

由图象可知：
当a＜0时，|f（x）|=a无解，
当a=0时，|f（x）|=a有3解，
当0＜a＜1时，|f（x）|=a有5解，
当1≤a＜e-1时，|f（x）|=a有4解，
当e-1≤a＜4时，|f（x）|=a有3解，
当a=4时，|f（x）|=a有2解，
当a＞4时，|f（x）|=a有1解．
故选D．

点评 本题考查了函数单调性的判断，函数零点的个数与函数图象的关系，属于中档题．