
(本题满分18分)本题共3小题,第(1)小题6分,第(2)小题6分,第(3)小题6分.
已知函数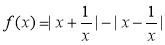 .
.
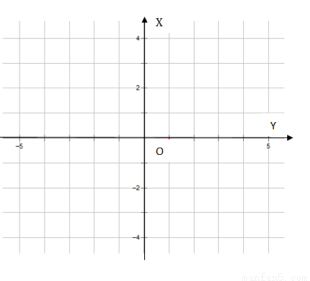
(1)指出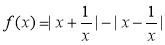 的基本性质(结论不要求证明)并作出函数
的基本性质(结论不要求证明)并作出函数 的图像;
的图像;
(2)关于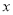 的不等式
的不等式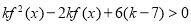 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)关于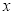 的方程
的方程 (
(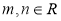 )恰有6个不同的实数解,求
)恰有6个不同的实数解,求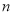 的取值范围.
的取值范围.
(1)见图象,(2) ,(3)
,(3)
【解析】
试题分析:明确绝对值的含义,首先化简绝对值符号,当 时,
时,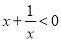 ,
,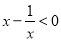 ,则
,则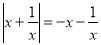 ,
,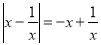 ,
,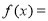
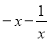
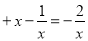 ,同理:当
,同理:当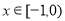 ,
,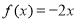 ,当
,当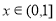 时,
时,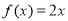 ,当
,当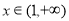 时,
时,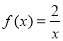 ,求出
,求出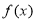 的解析式,画出函数
的解析式,画出函数 在每一段的图象,可以看出函数函数
在每一段的图象,可以看出函数函数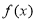 是偶函数,数形结合后,写出单调区间及最值;第二步先用换元法令
是偶函数,数形结合后,写出单调区间及最值;第二步先用换元法令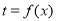 ,把不等式
,把不等式
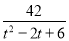 后,先求
后,先求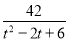 的最大值,然后写出
的最大值,然后写出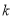 的范围;第三步先观察
的范围;第三步先观察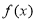 的图象可知
的图象可知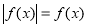 ,关于
,关于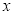 的方程
的方程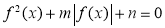 (
(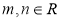 )恰有6个不同的实数解即
)恰有6个不同的实数解即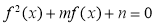 有6个不同的解,要使方程有6个不同实根,只需
有6个不同的解,要使方程有6个不同实根,只需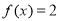 ,
,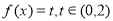 ,这时只需研究一元二次方程
,这时只需研究一元二次方程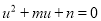 的根的分布问题即可,何时一元二次方程
的根的分布问题即可,何时一元二次方程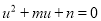 的一根为2,另一根在
的一根为2,另一根在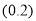 呢?设
呢?设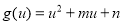 ,首先一根为2满足
,首先一根为2满足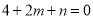 ,另一根在
,另一根在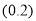 满足
满足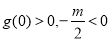
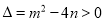 ,消去
,消去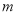 求出
求出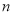 的取值范围即可 .
的取值范围即可 .
试题解析:(1)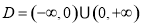 ,
, ,
,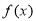 是偶函数,在区间
是偶函数,在区间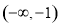 和
和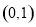 上单调递增,在区间
上单调递增,在区间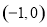 和
和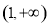 上单调递减,
上单调递减,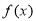 的最大值是
的最大值是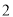 ,无最小值,值域为
,无最小值,值域为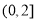
作图如下:
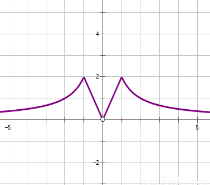
因为关于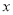 的不等式
的不等式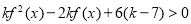 恒成立,令
恒成立,令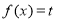 ,则
,则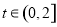 ,即不等式
,即不等式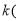
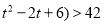 在
在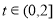 上恒成立,当
上恒成立,当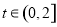 时,
时, ,不等式化为
,不等式化为
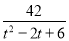 ,
,
又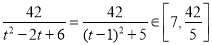
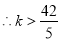
(3)关于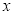 的方程
的方程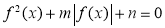 (
(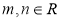 )恰有6个不同的实数解即
)恰有6个不同的实数解即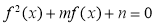 有6个不同的解,数形结合可知必有
有6个不同的解,数形结合可知必有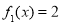 和
和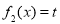 ,
,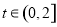 ,令
,令 ,则关于
,则关于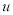 的方程
的方程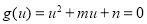 有一根为2,另一根在
有一根为2,另一根在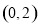 间,
间,

考点:1.含绝对值符号的函数式化为分段函数;2.极端原理;3.数形结合;


科目:高中数学 来源:2014-2015学年吉林省长春市高三质量监测(二)理科数学试卷(解析版) 题型:选择题
下面左图是某学习小组学生数学考试成绩的茎叶图,1号到16号同学的成绩依次为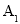 、
、 、
、 、
、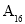 ,如图是统计茎叶图中成绩在一定范围内的学生人数的算法流程图,那么该算法流程图输出的结果是( )
,如图是统计茎叶图中成绩在一定范围内的学生人数的算法流程图,那么该算法流程图输出的结果是( )
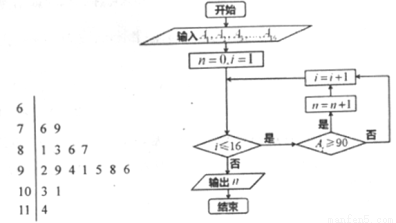
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省资阳市高三第二次诊断性考理科数学试卷(解析版) 题型:填空题
某年级有1000名学生,现从中抽取100人作为样本,采用系统抽样的方法,将全体学生按照1~1000编号,并按照编号顺序平均分成100组(1~10号,11~20号,…,991~1000号).若从第1组抽出的编号为6,则从第10组抽出的编号为_________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省资阳市高三第二次诊断性考理科数学试卷(解析版) 题型:选择题
有5名同学站成一排照相,则甲与乙且甲与丙都相邻的不同排法种数是 ( )
(A)8 (B)12
(C)36 (D)48
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市青浦区高三上学期期终学习质量调研数学试卷(解析版) 题型:选择题
设函数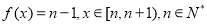 ,函数
,函数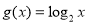 ,则方程
,则方程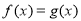 实数根的个数是( ).
实数根的个数是( ).
(A) 个 (B)
个 (B)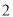 个 (C)
个 (C)  个 (D)
个 (D)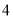 个
个
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省潍坊市高三上学期期末考试文科数学试卷B卷(解析版) 题型:填空题
设函数 的定义域为D,若任取
的定义域为D,若任取 ,存在唯一的
,存在唯一的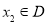 满足
满足 ,则称C为函数
,则称C为函数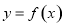 在D上的均值.给出下列五个函数:
在D上的均值.给出下列五个函数:
①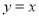 ;②
;② ;③
;③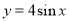 ;④
;④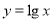 ;⑤
;⑤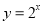 .则所有满足在其定义域上的均值为2的函数的序号为_________.
.则所有满足在其定义域上的均值为2的函数的序号为_________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省青岛市高三上学期期末考试文科数学试卷(解析版) 题型:选择题
已知函数 是偶函数,当
是偶函数,当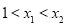 时,
时,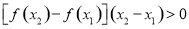 恒成立,设
恒成立,设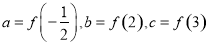 ,则
,则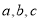 的大小关系为
的大小关系为
A. 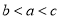 B.
B. 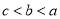 C.
C. 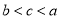 D.
D. 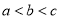
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com