
| ��x��y�������굥λ��km�� | 1��2��30�� | 2��4��40�� | 3��5��60�� | 4��6��50�� | 5��8��70�� | 6��1��y�� |
| ��̽��ȣ�km�� | 2 | 4 | 5 | 6 | 8 | 10 |
| ��������L�� | 40 | 70 | 110 | 90 | 160 | 205 |
���� ��1������ǰ5�����ݵõ�$\overline{x}$��$\overline{y}$���ɻع�ֱ�߷��̱ع�ƽ��㣨$\overline{x}$��$\overline{y}$���������y��
��2���ֱ����$\widehat{b}$��$\widehat{a}$��a��b���Ӷ��õ�$\frac{\widehat{b}-b}{b}��5%$��$\frac{\widehat{a}-a}{a}��8%$����������10%���ɴ�����������
��3�������⿱�����ʾ���X�Ŀ���ȡֵΪ2��3��4���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к�EX��
��� �⣺��1������ǰ5�����ݵõ�$\overline{x}$=$\frac{1}{5}$��2+4+5+6+8��=5��$\overline{y}$=$\frac{1}{5}$��30+40+60+50+70��=50��
�ع�ֱ�߷��̱ع�ƽ��㣨$\overline{x}$��$\overline{y}$����
��a=$\overline{y}-b\overline{x}$=50-6.5��5=17.5��
��ع�ֱ�߷���Ϊy=6.5x+17.5��
��x=1ʱ��y=6.5+17.5=24��
��y��Ԥ��ֵΪ24��
��2����$\overline{x}=4��\overline{y}=46.25$��$\sum_{i=1}^{4}{{x}_{2i-1}}^{2}$=94��$\sum_{i=1}^{4}{x}_{2i-1}{y}_{2i-1}$=945��
��$\widehat{b}$=$\frac{\sum_{i=1}^{4}{x}_{2i-1}{y}_{2i-1}-4\overline{x}\overline{y}}{\sum_{i=1}^{4}{{x}_{2i-1}}^{2}-4{\overline{x}}^{2}}$$\frac{945-4��4��46.25}{94-4��{4}^{2}}$��6.83��
$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$=46.25-6.83��4=18.93��
��$\widehat{b}$=6.83��$\widehat{a}$=18.93��b=6.85��a=17.5��
$\frac{\widehat{b}-b}{b}��5%$��$\frac{\widehat{a}-a}{a}��8%$����������10%��
��ʹ��λ����ӽ������оɾ�6��1��24����
��3�������⣬1��3��5��6��4�ھ������ʾ���2��4�����ھ��Ƿ����ʾ���
������ʾ���X�Ŀ���ȡֵΪ2��3��4��
P��X=2��=$\frac{{C}_{4}^{2}{C}_{2}^{2}}{{C}_{6}^{4}}$=$\frac{2}{5}$��
P��X=3��=$\frac{{C}_{4}^{3}{C}_{2}^{1}}{{C}_{6}^{4}}$=$\frac{8}{15}$��
P��X=4��=$\frac{{C}_{4}^{4}{C}_{2}^{0}}{{C}_{6}^{4}}$=$\frac{1}{15}$��
��X�ķֲ���Ϊ��
| X | 2 | 3 | 4 |
| P | $\frac{2}{5}$ | $\frac{8}{15}$ | $\frac{1}{15}$ |
���� ���⿼�����Իع鷽�̵�Ӧ�ã�������ɢ����������ķֲ��м���ѧ�����������е��⣬����ʱҪ�������⣬ע���������֪ʶ�ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{6}}{2}$ | B�� | $\frac{\sqrt{6}}{3}$ | C�� | $\frac{\sqrt{6}}{4}$ | D�� | $\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
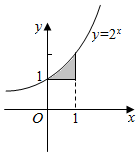
| A�� | ${��}_{0}^{1}$2xdx | B�� | ${��}_{0}^{1}$��2x-1��dx | C�� | ${��}_{0}^{1}$��2x+1��dx | D�� | ${��}_{0}^{1}$��1-2x��dx |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
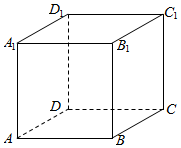 ��ͼ��ʾ�����ⳤΪ1��������ABCD-A1B1C1D1�У�
��ͼ��ʾ�����ⳤΪ1��������ABCD-A1B1C1D1�У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com