
分析 (1)明确目标函数几何意义,目标函数表示动点(x,y)与定点P(-1,-2)连线斜率,过P做直线与可行域相交可计算出直线斜率,从而得出所求目标函数范围;
(2)首先求出z=x+2y-4的范围,然后求绝对值的范围.
解答 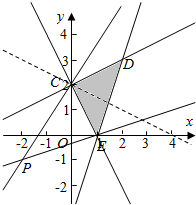 解:不等式组对应的平面区域如图
解:不等式组对应的平面区域如图
(1)表示可行域内任一点(x,y)与定点P(-2,-1)连线的斜率.
由图可知,kPE≤k≤kPC.
由$\left\{\begin{array}{l}{2x+y-2=0}\\{3x-y-3=0}\end{array}\right.$得E(1,0).由$\left\{\begin{array}{l}{x-2y+4=0}\\{3x-y-3=0}\end{array}\right.$得D(2,3)
∴kPE=$\frac{1}{3}$,kPC=$\frac{3}{2}$,故z的最小值为$\frac{1}{3}$,最大值为$\frac{3}{2}$.
(2)由图可知z=x+2y-4过E时最小为-3,过D时最大为4,
所以z=|x+2y-4|最小值为0,最大值为4.
点评 本题主要考查了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题.目标函数有唯一最优解是最常见的问题,这类问题一般要分三步:画出可行域、求出关键点、定出最优解.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
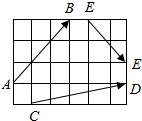 图中,小正方形的边长为1,则|$\overrightarrow{AB}$|=$3\sqrt{2}$,|$\overrightarrow{CD}$|=$\sqrt{26}$,|$\overrightarrow{EF}$|=$2\sqrt{2}$.
图中,小正方形的边长为1,则|$\overrightarrow{AB}$|=$3\sqrt{2}$,|$\overrightarrow{CD}$|=$\sqrt{26}$,|$\overrightarrow{EF}$|=$2\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com