练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设集合A＝{x|x2－2x＋2m＋4＝0}，B＝{x|x<0}．若A∩B≠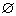，求实数m的取值范围．


    解：(解法1)据题意知方程x2－2x＋2m＋4＝0至少有一个负实数根．

    设M＝{m|关于x的方程x2－2x＋2m＋4＝0两根均为非负实数}，

    则

    ∴ M＝.

    设全集U＝{m|Δ≥0}＝，

    ∴ m的取值范围是∁UM＝{m|m<－2}．

    (解法2)方程的小根x＝1－<0

    >1－2m－3>1m<－2.

    (解法3)设f(x)＝x2－2x＋4，这是开口向上的抛物线．因为其对称轴x＝1>0，则据二次函数性质知命题又等价于f(0)<0m<－2.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知双曲线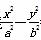＝1(a＞0，b＞0)的左、右焦点分别为F1，F2，点O为双曲线的中心，点P在双曲线右支上，△PF1F2内切圆的圆心为Q，圆Q与x轴相切于点A，过F2作直线PQ的垂线，垂足为B，则下列结论成立的是(　　)

    A．|OA|＞|OB|                   B．|OA|＜|OB|

    C．|OA|＝|OB|                   D．|OA|与|OB|大小关系不确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设集合A＝{x|x＝5－4a＋a2，a∈R}，B＝{y|y＝4b2＋4b＋2，b∈R}，则A、B的关系是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知集合A＝{x|(x－2)[x－(3a＋1)]＜0}，

    B＝.

    (1) 当a＝2时，求A∩B；

    (2) 求使B真包含于A的实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若全集U＝{1，2，3，4，5，6}，M＝{2，3}，N＝{1，4}，则(∁UM)∩(∁UN)＝________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     设P和Q是两个集合，定义集合P－Q＝{x|x∈P，且xQ}，如果P＝{x|log2x<1}，Q＝{x||x－2|<1}，那么P－Q＝________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知p、q是r的充分条件，r是s的充分条件，q是s的必要条件，则s是p的__________条件．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     在命题p的四种形式的命题(原命题、逆命题、否命题、逆否命题)中，正确命题的个数记为f(p)，已知命题p：“若两条直线l1：a1x＋b1y＋c1＝0，l2：a2x＋b2y＋c2＝0平行，则a1b2－a2b1＝0”．那么f(p)＝________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知正项数列{an}，其前n项和Sn满足6Sn＝a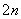＋3an＋2，且a1，a2，a6是等比数列{bn}的前三项．

    (1)求数列{an}与{bn}的通项公式；

    (2)记Tn＝a1bn＋a2bn－1＋…＋anb1，n∈N*，证明：3Tn＋1＝2bn＋1－an＋1(n∈N*)．

    查看答案和解析>>

    同步练习册答案