
【题目】已知函数![]() ,且
,且![]() ,则
,则 ![]() 的值( )
的值( )
A. 恒为正数 B. 恒等于零
C. 恒为负数 D. 可能大于零,也可能小于零
【答案】C
【解析】
根据函数的解析式可得函数是奇函数,并且根据函数解析式可得函数是减函数,所以根据题意α+β>0,β+γ>0,γ+α>0,可得α>﹣β,β>﹣γ,γ>﹣α,进而结合函数的奇偶性与函数的单调性即可得到答案.
由题意可得:函数f(x)=﹣x﹣x3,
所以函数的定义域为R,并且有f(﹣x)=x+x3=﹣f(x)
所以函数f(x)是定义域内的奇函数.
因为﹣x是减函数,﹣x3也是减函数,所以函数f(x)=﹣x﹣x3在R上是减函数.
因为实数α、β、γ满足α+β>0,β+γ>0,γ+α>0,
所以α>﹣β,β>﹣γ,γ>﹣α,
所以f(α)<f(﹣β)=﹣f(β)…①,
f(β)<f(﹣γ)=﹣f(γ)…②,
f(γ)<f(﹣α)=﹣f(α)…③,
①+②+③并且整理可得:f(α)+f(β)+f(γ)<0.
故选:C.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)在R上的导函数为f'(x),对于任意的实数x,都有f'(x)+2017<4034x,若f(t+1)<f(﹣t)+4034t+2017,则实数t的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小型企业甲产品生产的投入成本![]() (单位:万元)与产品销售收入
(单位:万元)与产品销售收入![]() (单位:万元)存在较好的线性关系,下表记录了最近5次产品的相关数据.
(单位:万元)存在较好的线性关系,下表记录了最近5次产品的相关数据.
| 7 | 10 | 11 | 15 | 17 |
| 19 | 22 | 25 | 30 | 34 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)根据(1)中的回归方程,判断该企业甲产品投入成本20万元的毛利率更大还是投入成本24万元的毛利率更大(![]() )?
)?
相关公式: 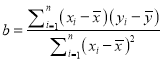
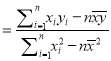 ,
, ![]() .
.
【答案】(1)![]() .(2)投入成本20万元的毛利率更大.
.(2)投入成本20万元的毛利率更大.
【解析】试题分析:(1)由回归公式,解得线性回归方程为![]() ;(2)当
;(2)当![]() 时,
时, ![]() ,对应的毛利率为
,对应的毛利率为![]() ,当
,当![]() 时,
时, ![]() ,对应的毛利率为
,对应的毛利率为![]() ,故投入成本20万元的毛利率更大。
,故投入成本20万元的毛利率更大。
试题解析:
(1)![]() ,
, ![]() ,
,
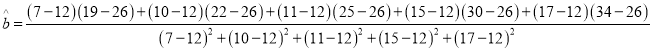
![]() ,
, ![]() ,故
,故![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() .
.
(2)当![]() 时,
时, ![]() ,对应的毛利率为
,对应的毛利率为![]() ,
,
当![]() 时,
时, ![]() ,对应的毛利率为
,对应的毛利率为![]() ,
,
故投入成本20万元的毛利率更大.
【题型】解答题
【结束】
21
【题目】已知椭圆![]() 的一个焦点为
的一个焦点为![]() .设椭圆
.设椭圆![]() 的焦点恰为椭圆
的焦点恰为椭圆![]() 短轴的顶点,且椭圆
短轴的顶点,且椭圆![]() 过点
过点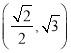 .
.
(1)求![]() 的方程及离心率;
的方程及离心率;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人的各科成绩如图中的茎叶图所示,则下列说法不正确的是( )
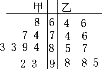
A. 甲、乙两人的各科平均分相同
B. 甲各科成绩的中位数是83,乙各科成绩的中位数是85
C. 甲各科成绩比乙各科成绩稳定
D. 甲各科成绩的众数是89,乙各科成绩的众数为87
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下三个关于圆锥曲线的命题中:
①设A、B为两个定点,K为非零常数,若|PA|-|PB|=K,则动点P的轨迹是双曲线.
②方程![]() 的两根可分别作为椭圆和双曲线的离心率.
的两根可分别作为椭圆和双曲线的离心率.
③双曲线![]() 与椭圆
与椭圆![]() 有相同的焦点.
有相同的焦点.
④已知抛物线![]() ,以过焦点的一条弦AB为直径作圆,则此圆与准线相切.
,以过焦点的一条弦AB为直径作圆,则此圆与准线相切.
其中真命题为_________(写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2+2x-4y+3=0.
(1)若直线l过点(-2,0)且被圆C截得的弦长为2,求直线l的方程;
(2)从圆C外一点P向圆C引一条切线,切点为M,O为坐标原点,且|PM|=|PO|,求|PM|的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com