
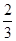 ,乙的命中率为P2,在射击比赛活动中每人射击两发子弹则完成一次检测,在一次检测中,若两人命中数相等且都不少于一发,则称该射击小组为“先进和谐组”.
,乙的命中率为P2,在射击比赛活动中每人射击两发子弹则完成一次检测,在一次检测中,若两人命中数相等且都不少于一发,则称该射击小组为“先进和谐组”.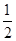 ,求该小组在一次检测中荣获“先进和谐组”的概率;
,求该小组在一次检测中荣获“先进和谐组”的概率; 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:高中数学 来源:不详 题型:解答题
| 组号 | 分组 | 频数 | 频率 |
| 第一组 | [160,165) | 5 | 0.05 |
| 第二组 | [165,170) | 35 | 0.35 |
| 第三组 | [170,175) | 30 | a |
| 第四组 | [175,180) | b | 0.2 |
| 第五组 | [180,185) | 10 | 0.1 |
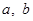 的值;
的值; 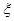 ,求
,求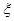 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| 2i |
| 1-i |
| C | 12013 |
| C | 22013 |
| C | 32013 |
| C | 20132013 |
| A.i | B.-i | C.-1+i | D.1+i |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.Y的取值为0,1,2,3 |
| B.P(Y=0)+P(Y=1)+P(Y=2)+P(Y=3)=1 |
| C.若每录取1人学校奖励300元给班主任,没有录取不奖励,则班主任得奖金数为300Y |
| D.若每不录取1人学校就扣班主任300元,录取不奖励,则班主任得奖金数为-300Y |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
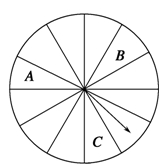
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com