
���� ��I���������������Һ�������������æأ��ٰ���֪������������æգ��Ӷ��õ�����f��x������ʽ���ٸ������Һ����ĵ�������ú���f��x���ĵ����������䣮
��II����x��A�����f��x����[1��2]���ٸ���A⊆B���ɵ� $\left\{\begin{array}{l}{m-1��1}\\{m+1��2}\end{array}\right.$���Ӷ����m�ķ�Χ��
��III������������� cos��+sin��=$\frac{2}{3}$��ƽ���ɵ�sin��cos����ֵ���ٻ���Ҫ���ʽ�ӣ���������ֵ���룬�ɵ�Ҫ��ʽ�ӵ�ֵ��
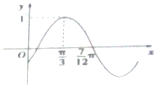
��� �⣺��I��������ɵú���������Ϊ$\frac{2��}{��}$=2��$\frac{��}{2}$����æ�=2���ٰѵ㣨$\frac{5��}{12}$��2�����뺯��f��x��=2sin��2x+�գ���
�ɵ�sin��2��$\frac{5��}{12}$+�գ�=1����2��$\frac{5��}{12}$+��=2k��+$\frac{��}{2}$��k��z��
�ٽ�ϣ�0��|��|��$\frac{��}{2}$���ɵæ�=-$\frac{��}{3}$��f��x��=2sin��2x-$\frac{��}{3}$����
��2k��-$\frac{��}{2}$��2x-$\frac{��}{3}$��2k��+$\frac{��}{2}$��k��z�����k��-$\frac{��}{12}$��x��k��+$\frac{5��}{12}$��
�ʺ���f��x���ĵ�����������Ϊ[k��-$\frac{��}{12}$��k��+$\frac{5��}{12}$]��k��z��
��II����A={x|$\frac{��}{4}$��x��$\frac{��}{2}$}��B={x||f��x��-m|��1}={x|m-1��f��x����m+1}��
����$\frac{��}{4}$��x��$\frac{��}{2}$ʱ��2x-$\frac{��}{3}$��[$\frac{��}{6}$��$\frac{2��}{3}$]����f��x����[1��2]��
����A⊆B����$\left\{\begin{array}{l}{m-1��1}\\{m+1��2}\end{array}\right.$����1��m��2��
��III����cos��+$\frac{1}{2}$f��$\frac{��}{2}$+$\frac{��}{6}$��=cos��+sin[2��$\frac{��}{2}$+$\frac{��}{6}$��-$\frac{��}{3}$]=cos��+sin��=$\frac{2}{3}$��ƽ���ɵ�sin��cos��=-$\frac{5}{18}$��
��$\frac{\sqrt{2}sin��2��-\frac{��}{4}��+1}{1+tan��}$=$\frac{\sqrt{2}•cos����\frac{\sqrt{2}}{2}sin2��-\frac{\sqrt{2}}{2}cos2����+cos��}{cos��+sin��}$=$\frac{cos����sin2��-cos2��+1��}{\frac{2}{3}}$=$\frac{3}{2}$•cos����2sin��cos��+2sin2����
=3sin��cos����cos��+sin����=3����-$\frac{5}{18}$����$\frac{2}{3}$=-$\frac{5}{9}$��
���� ������Ҫ�������Һ��������ԡ������ԡ��������ֵ�����Ǻ�ȱ任�����ϼ�IJ�����ϵ��������ת������ѧ˼�룬�����е��⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��x+$\frac{1}{x}$����=1+$\frac{1}{{x}^{2}}$ | B�� | $��\frac{{e}^{x}}{x}����$=$\frac{{e}^{x}+x{e}^{x}}{{x}^{2}}$ | ||
| C�� | ��x2sinx����=2xcosx | D�� | ��log2x����=$\frac{1}{xln2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ǰ������½��۴� | B�� | Сǰ������½��۴� | ||
| C�� | ������ʽ�����½��۴� | D�� | ��ǰ���Сǰ�ᶼ�����½��۴� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com