
分析 根据导数的公式进行求导即可.
解答 解:(1)y′=3(x3+1)2(3x2)=9(x3+1)2•x2,
y′′=9[(x3+1)2]′•x2+9(x3+1)2•2x
=18(x3+1)•x2+18(x3+1)2=18(x3+1)(x3+x2+1),
(2)y′=ex+cosx,y′′=ex-sinx;
(3)y′=cosx-xsinx,y′′=-cosx-(sinx+xcosx)=-cosx-sinx-xcosx;
(4)y′=2x•ln2,y′′=2x•(ln2)2,
(5)y′=2xlnx+x2•$\frac{1}{x}$=2xlnx+x,y′′=2lnx+2x•$\frac{1}{x}$+1=2lnx+2+2=3+2lnx;
(6)y=$\frac{x-1}{x+1}$=$\frac{x+1-2}{x+1}$=1-$\frac{2}{x+1}$,
则y′=$\frac{2}{(x+1)^{2}}$,y′′=-$\frac{4}{(x+1)^{3}}$.
点评 本题主要考查导数的计算,根据导数的公式是解决本题的关键.考查学生的运算能力.


科目:高中数学 来源: 题型:选择题
| A. | -8 | B. | -4 | C. | -6 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
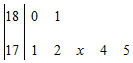 (文科)某校女子篮球队7名运动员身高(单位:厘米)分布的茎叶图如图,已知记录的平均身高为175cm,但记录中有一名运动员身高的末位数字不清晰,如果把其末尾数记为x,那么x的值为2.
(文科)某校女子篮球队7名运动员身高(单位:厘米)分布的茎叶图如图,已知记录的平均身高为175cm,但记录中有一名运动员身高的末位数字不清晰,如果把其末尾数记为x,那么x的值为2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 6 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com