
【题目】设函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .
.
(1)求![]() ;
;
(2)若![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,求满足
时,求满足![]() 的
的![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)详见解析;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】试题分析:(1)由对称轴的位置,分类讨论得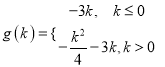 ;(2)
;(2)![]() ,得
,得![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() ;(3)因为
;(3)因为![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() ,所以
,所以![]() 即
即![]() 设
设![]() ,讨论单调性知函数
,讨论单调性知函数![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
.解法一:(Ⅰ)由题意知,函数![]() 的图像为开口向上的抛物线,且对称轴为
的图像为开口向上的抛物线,且对称轴为![]() ,
,
当![]() 时,函数
时,函数![]() 在
在![]() 单调递增,则
单调递增,则![]() ,
,
当![]() 时,函数
时,函数![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,则
单调递增,则![]() ,
,
所以, 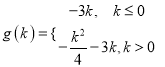
(Ⅱ)![]() ,
, ![]()
![]() ,即
,即![]() 在
在![]() 上恒成立,
上恒成立,
设![]() ,
, ![]() ,则
,则
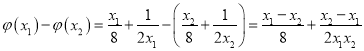
![]()
![]() ,
,![]() ,又
,又![]() ,
,![]()
![]() ,即
,即![]()
![]() 函数
函数![]() 在
在![]() 上单调递减,
上单调递减,
![]() ,
,![]() .
.
(Ⅲ)![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() ,
,
∴![]() 即
即![]()
设![]() ,则其定义域为
,则其定义域为![]()
设![]() ,易得该函数在
,易得该函数在![]() 上单调递减,
上单调递减,
设![]() ,由
,由![]() 知,该函数也在
知,该函数也在![]() 上单调递减,
上单调递减,
由上可知函数![]() 在
在![]() 上单调递减,
上单调递减,
又![]()
所以![]()
即满足条件的![]() 的取值范围为
的取值范围为![]() .
.
解法二:(Ⅰ)同法一
(Ⅱ)因为![]() 所以
所以![]() ,
,
由![]() ,得
,得![]() ,
,
设![]() ,题意等价于:
,题意等价于:
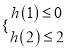 ,即
,即![]()
解得: ![]()
(Ⅲ)![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]()
∴![]() 即
即![]()
![]() ,即
,即![]() ,
,
设![]() 其对称轴
其对称轴![]() ,开口向下,
,开口向下,
所以![]() 在
在![]() 单调递增,
单调递增,
设![]()
![]() 在
在![]() 单调递减,且
单调递减,且![]() ,
,
所以,满足条件的![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,A,B,C三点满足![]() 。
。
(1)求证:A,B,C三点共线;
(2)若A(1,cosx),B(1+sinx,cosx),且x∈[0, ![]() ],函数f(x)=
],函数f(x)=![]() (2m+
(2m+![]() )|
)|![]() |+m2的最小值为5,求实数m的值。
|+m2的最小值为5,求实数m的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2-2x+4y-4=0,
(1)求圆C关于直线![]() 对称的圆的方程;
对称的圆的方程;
(2)问是否存在斜率为1的直线l,使l被圆C截得弦AB,且以AB为直径的圆经过点![]() ?若存在,求出直线l的方程;若不存在,说明理由.
?若存在,求出直线l的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国科学院亚热带农业生态研究所2017年10月16日正式发布一种水稻新种质,株高可达2.2米以上,具有高产、抗倒伏、抗病虫害、酎淹涝等特点,被认为开启了水稻研制的一扇新门.以下是![]() 两组实验田中分别抽取的6株巨型稻的株高,数据如下(单位:米).
两组实验田中分别抽取的6株巨型稻的株高,数据如下(单位:米).
![]() : 1.7 1.8 1.9 2.2 2.4 2.5
: 1.7 1.8 1.9 2.2 2.4 2.5
![]() : 1.8 1.9 2.0 2.0 2.4 2.5
: 1.8 1.9 2.0 2.0 2.4 2.5
(1)绘制![]() 两组数据的茎叶图,并求出
两组数据的茎叶图,并求出![]() 组数据的中位数和
组数据的中位数和![]() 组数据的方差;
组数据的方差;
(2)从![]() 组样本中随机抽取2株,请列出所有的基本事件,并求至少有一株超过
组样本中随机抽取2株,请列出所有的基本事件,并求至少有一株超过![]() 组株高平均值的概率.
组株高平均值的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】宁德被誉为“中国大黄鱼之乡”,海域面积4.46万平方公里,水产资源极为丰富.“宁德大黄鱼”作为福建宁德地理标志产品,同时也是宁德最具区域特色的海水养殖品种,全国80%以上的大黄鱼产自宁德,年产值超过60亿元.现有一养殖户为了解大黄鱼的生长状况,对其渔场中100万尾鱼的净重(单位:克)进行抽样检测,将抽样所得数据绘制成频率分布直方图如图.其中产品净重的范围是![]() ,已知样本中产 品净重小于100克的有360尾.
,已知样本中产 品净重小于100克的有360尾.

(1)计算样本中大黄鱼的数量;
(2)假设样本平均值不低于101.3克的渔场为![]() 级渔场,否则为
级渔场,否则为![]() 级渔场.那么要使得该渔场为
级渔场.那么要使得该渔场为![]() 级渔场,则样本中净重在
级渔场,则样本中净重在![]() 的大黄鱼最多有几尾?
的大黄鱼最多有几尾?
(3)为提升养殖效果,该养殖户进行低沉性配合饲料养殖,净重小于98克的每4万尾合用一个网箱,大于等于98克的每3万尾合用一个网箱.根据(2)中所求的最大值,估计该养殖户需要准备多少个网箱?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图是正方体的平面展开图,在这个正方体中:① ![]() 与
与 ![]() 平行;②
平行;② ![]() 与
与 ![]() 是异面直线;③
是异面直线;③ ![]() 与
与 ![]() 成
成 ![]() 角;④
角;④ ![]() 与
与 ![]() 垂直;以上四个命题中,正确的是( )
垂直;以上四个命题中,正确的是( )
A.①②③
B.②④
C.②③④
D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系 ![]() 中,曲线
中,曲线 ![]() 的参数方程为
的参数方程为 ![]() (
( ![]() 为参数),直线
为参数),直线 ![]() 的方程为
的方程为 ![]() ,以
,以 ![]() 为极点,以
为极点,以 ![]() 轴正半轴为极轴,建立极坐标系,
轴正半轴为极轴,建立极坐标系,
(1)求曲线 ![]() 和直线
和直线 ![]() 的极坐标方程;
的极坐标方程;
(2)若直线 ![]() 与曲线
与曲线 ![]() 交于
交于 ![]() 两点,求
两点,求 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
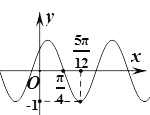
【题目】函数![]() (其中
(其中![]() )的部分图象如图所示,为了得到
)的部分图象如图所示,为了得到![]() 的图象,只要将
的图象,只要将![]() 的图象
的图象
A. 先向右平移![]() 个单位长度,再把所得各点的横坐标伸长到原来的
个单位长度,再把所得各点的横坐标伸长到原来的![]() 倍,纵坐标不变
倍,纵坐标不变
B. 先向右平移![]() 个单位长度,再把所得各点的横坐标伸长到原来的
个单位长度,再把所得各点的横坐标伸长到原来的![]() 倍,纵坐标不变
倍,纵坐标不变
C. 先向左平移![]() 个单位长度 ,再把所得各点的横坐标缩短到原来的
个单位长度 ,再把所得各点的横坐标缩短到原来的![]() 倍,纵坐标不变
倍,纵坐标不变
D. 先向左平移![]() 个单位长度, 再把所得各点的横坐标缩短到原来的
个单位长度, 再把所得各点的横坐标缩短到原来的![]() 倍,纵坐标不变
倍,纵坐标不变
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com