
已知直三棱柱 中,
中, ,
,
 是
是 中点,
中点,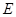 是
是 中点.
中点.
(1)求三棱柱 的体积;
的体积;
(2)求证: ;
;
(3)求证: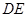 ∥面
∥面 .
.
(1)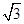 ;(2)证明详见解析;(3)证明详见解析.
;(2)证明详见解析;(3)证明详见解析.
解析试题分析:(1)这是一个直三棱柱,直接由体积计算公式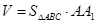 即可求解;(2)要证
即可求解;(2)要证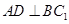 ,只须证明
,只须证明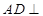 面
面 ,注意到面
,注意到面 与底面
与底面 垂直且交线为
垂直且交线为 ,而依题意又有
,而依题意又有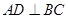 ,由面面垂直的性质可得
,由面面垂直的性质可得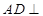 面
面 ,问题得证;(3)要证
,问题得证;(3)要证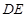 ∥面
∥面 ,有两种思路:一是在平面
,有两种思路:一是在平面 内找一条直线与
内找一条直线与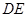 平行,这时只须取
平行,这时只须取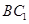 的中点
的中点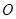 ,连接
,连接 ,证明四边形
,证明四边形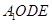 为平行四边形即可;二是先证经过直线
为平行四边形即可;二是先证经过直线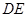 的一个平面与面
的一个平面与面 平行,这时可取
平行,这时可取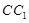 中点
中点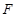 ,连结
,连结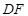 ,
,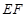 ,先证明面
,先证明面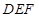 ∥面
∥面 ,再由面面平行的性质即可证明
,再由面面平行的性质即可证明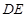 ∥面
∥面 .
.
试题解析:(1) 3分
3分
(2)∵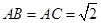 ,∴
,∴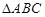 为等腰三角形
为等腰三角形
∵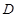 为
为 中点,∴
中点,∴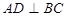 -4分
-4分
∵ 为直棱柱,∴面
为直棱柱,∴面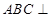 面
面 5分
5分
∵面 面
面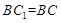 ,
,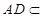 面
面
∴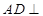 面
面 6分
6分
∴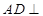
 7分
7分
(3)取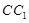 中点
中点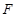 ,连结
,连结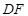 ,
,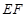 8分
8分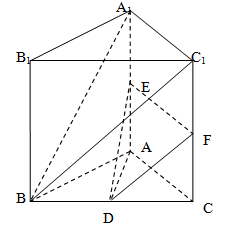
∵ 分别为
分别为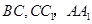 的中点
的中点
∴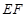 ∥
∥ ,
,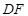 ∥
∥ , 9分
, 9分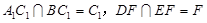
∴面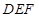 ∥面
∥面 11分
11分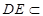 面
面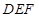


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝.再用S平方米塑料片制成圆柱的侧面和下底面(不安装上底面).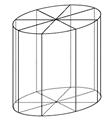
(1)当圆柱底面半径r取何值时,S取得最大值?并求出该最大值(结果精确到0.01平方米).
(2)若要制作一个如图放置的、底面半径为0.3米的灯笼,请作出灯笼的三视图(作图时,不需考虑骨架等因素).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个几何体是由圆柱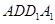 和三棱锥
和三棱锥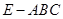 组合而成,点
组合而成,点 、
、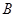 、
、 在圆
在圆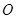 的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图4所示,其中
的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图4所示,其中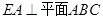 ,
,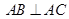 ,
,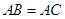 ,
, .
.
(1)求证: ;
;
(2)求三棱锥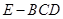 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知一个四棱锥P-ABCD的三视图(正视图与侧视图为直角三角形,俯视图是带有一条对角线的正方形)如图,E是侧棱PC的中点.
(1)求四棱锥P-ABCD的体积;
(2)求证:平面APC⊥平面BDE.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,在四棱锥P-ABCD中,△PBC为正三角形,PA⊥底面ABCD,其三视图如图所示,俯视图是直角梯形.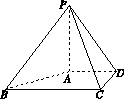
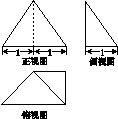
(1)求正视图的面积;
(2)求四棱锥P-ABCD的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com