Question

19．空间四边形ABCD中，对角线AC与BD互相垂直，那么顺次联结四边形各边中点所得的四边形是矩形．

Answer 1

分析 根据三角形中位线的性质，可得到这个四边形是平行四边形，再由对角线垂直，能证出有一个角等于90°，则这个四边形为矩形．

解答 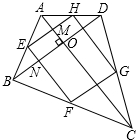已知：AC⊥BD，E、F、G、H分别为各边的中点，连接点E、F、G、H．
求证：四边形EFGH是矩形
证明：∵E、F、G、H分别为各边的中点，
∴EF∥AC，GH∥AC，EH∥BD，FG∥BD，（三角形的中位线平行于第三边）
∴四边形EFGH是平行四边形，（两组对边分别平行的四边形是平行四边形）
∵AC⊥BD，EF∥AC，EH∥BD，
∴∠EMO=∠ENO=90°，
∴四边形EMON是矩形（有三个角是直角的四边形是矩形），
∴∠MEN=90°，
∴四边形EFGH是矩形（有一个角是直角的平行四边形是矩形）．
故答案为：矩形．

点评 本题考查的是矩形的判定方法，常用的方法有三种：
①一个角是直角的平行四边形是矩形．
②三个角是直角的四边形是矩形．
③对角线相等的平行四边形是矩形．