练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知正实数x，y满足
    2
    x
    +
    1
    y
    =1，若m=x+y，则实数m的取值范围是
     
    ．
    考点：基本不等式在最值问题中的应用
    专题：计算题,不等式的解法及应用
    分析：由
    2
    x
    +
    1
    y
    =1，化m=x+y=（x+y）（
    2
    x
    +
    1
    y
    ）=3+
    2y
    x
    +
    x
    y
    ，从而利用基本不等式．
    解答： 解：∵
    2
    x
    +
    1
    y
    =1，
    ∴m=x+y=（x+y）（
    2
    x
    +
    1
    y
    ）
    =3+
    2y
    x
    +
    x
    y
    ≥3+2
    		2
    ，
    （当且仅当x=2+
    		2
    ，y=
    		2
    +1时，等号成立）
    故实数m的取值范围是[3+2
    		2
    ，+∞）．
    故答案为：[3+2
    		2
    ，+∞）．
    点评：本题考查了基本不等式的应用，属于中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    用诱导公式求下列三角函数值．
    （1）cos
    65
    6
    π；
    （2）sin（-
    31
    4
    π）；
    （3）tan（-
    26π
    3
    ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知椭圆的中心在原点，对称轴为坐标轴，F1、F2为焦点，点P在椭圆上，直线PF1与PF2的倾斜角的差为90°，△F1PF2的面积是20，离心率为
    		5
    3
    ，求椭圆的标准方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知抛物线C：y2=2px（p＞0）的焦点为F，若过点F且斜率为1的直线与抛物线相交于M，N两点，且|MN|=8．
    （Ⅰ）求抛物线C的方程；
    （Ⅱ）设直线l为抛物线C的切线且l∥MN，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    给出下列四个命题：
    ①动点P到A（-5，0）的距离与它到B（5，0）距离的差等于6，则点P的轨迹是双曲线；
    ②“直线与双曲线只有一个公共点”是“直线与双曲线相切”的必要不充分条件；
    ③直线l交椭圆3x2+4y2=48于A，B两点，AB的中点为M（2，1），则l的斜率为-
    3
    2
    ；
    ④已知动圆P过定点A（-3，0），并且与定圆B：（x-3）2+y2=64内切，则动圆的圆心P的轨迹是椭圆．
    其中正确的命题为
     
    （只填正确命题的序号）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下面四个命题中的真命题是（　　）
    A、命题“?x≥2，均有x2-3x+2≥0”的否定是：“?x＜2，使得x2-3x+2＜0”
    B、命题“若x2=1，则x=1”的否命题为“若x2=1，则x≠1”
    C、采用系统抽样法从某班按学号抽取5名同学参加活动，学号为5、16、27、38、49的同学均被选出，则该班人数可能为60
    D、在某项测量中，测量结果X服从正态分布N（1，σ2）（σ＞0），若X在（0，1）内取值的概率为0.4，则X在（0，2）内取值的概率为0.8

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    将下列圆的方程化为标准方程，并写出圆心和半径．
    （1）x2+y2+4x-6y-12=0
    （2）4x2+4y2-8x+4y-15=0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

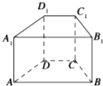    如图所示，在直四棱柱ABCD-A1B1C1D1中，当底面四边形A1B1C1D1满足条件
     
    时，有A1C⊥B1D1（注：填上你认为正确的一种情况即可，不必考虑所有可能的情况）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若不等式x2+kx+1＜0的解集为空集，则k的取值范围是（　　）
    A、[-2，2]
    B、（-∞，-2]∪[2，+∞）
    C、（-2，2）
    D、（-∞，-2）∪（2，+∞）

    查看答案和解析>>

    同步练习册答案