
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
分析 由题意知试验发生包含的所有事件是6,事件A和事件B是互斥事件,看出事件A和事件B包含的基本事件数,根据互斥事件和古典概型概率公式得到结果.
解答 解:∵事件B表示“小于5的点数出现”,
∴B的对立事件是“大于或等于5的点数出现”,
∴表示事件是出现点数为5和6.
∵事件A表示“小于5的偶数点出现”,
它包含的事件是出现点数为2和4,
∴P(A∪$\overline{B}$)=$\frac{1}{3}$+$\frac{1}{3}$=$\frac{2}{3}$.
故选:C.
点评 本题考查互斥事件和对立事件的概率,分清互斥事件和对立事件之间的关系,互斥事件是不可能同时发生的事件,对立事件是指一个不发生,另一个一定发生的事件.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{39}{79}$ | B. | $\frac{1}{80}$ | C. | $\frac{1}{2}$ | D. | $\frac{41}{80}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
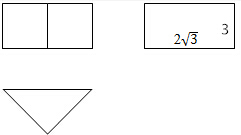 若一个三棱柱ABC-A1B1C1的三视图如图所示,主视图与左视图均为矩形,俯视图为一个正三角形.
若一个三棱柱ABC-A1B1C1的三视图如图所示,主视图与左视图均为矩形,俯视图为一个正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
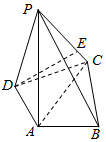 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AB,AD⊥DC,∠DAC=60°,PA=AC=2,AB=1.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AB,AD⊥DC,∠DAC=60°,PA=AC=2,AB=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com