
已知函数f(x)=ax2-(a+2)x+lnx.
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)当a>0时,若f(x)在区间[1,e]上的最小值为-2,求a的取值范围.
(1)y=-2 (2)[1,+∞)
【解析】【解析】
(1)当a=1时,f(x)=x2-3x+lnx,f′(x)=2x-3+ .
.
因为f′(1)=0,f(1)=-2,
所以切线方程是y=-2.
(2)函数f(x)=ax2-(a+2)x+lnx的定义域是(0,+∞).
当a>0时,f′(x)=2ax-(a+2)+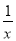 =
=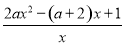 (x>0).
(x>0).
令f′(x)=0,即f′(x)=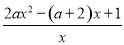 =
=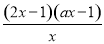 =0,
=0,
得x=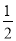 或x=
或x=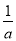 .
.
当0<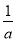 ≤1,即a≥1时,f(x)在[1,e]上单调递增,
≤1,即a≥1时,f(x)在[1,e]上单调递增,
所以f(x)在[1,e]上的最小值是f(1)=-2;
当1<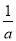 <e时,f(x)在[1,e]上的最小值f(
<e时,f(x)在[1,e]上的最小值f(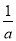 )<f(1)=-2,不合题意;
)<f(1)=-2,不合题意;
当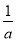 ≥e时,f(x)在[1,e]上单调递减.
≥e时,f(x)在[1,e]上单调递减.
所以f(x)在[1,e]上的最小值f(e)<f(1)=-2,不合题意.
综上a的取值范围为[1,+∞).


科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-2函数的单调性与最值(解析版) 题型:解答题
已知函数f(x)=a-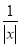 .
.
(1)求证:函数y=f(x)在(0,+∞)上是增函数;
(2)若f(x)<2x在(1,+∞)上恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-1函数的概念、定义域和值域(解析版) 题型:解答题
已知函数f(x)=x2-4ax+2a+6,x∈R.
(1)若函数的值域为[0,+∞),求a的值;
(2)若函数的值域为非负数集,求函数f(a)=2-a|a+3|的值域.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-1函数的概念、定义域和值域(解析版) 题型:选择题
若f(x)对于任意实数x恒有2f(x)-f(-x)=3x+1,则f(x)=( )
A.x-1 B.x+1 C.2x+1 D.3x+3
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-12导数的应用二(解析版) 题型:填空题
函数f(x)=-x3+mx2+1(m≠0)在(0,2)内的极大值为最大值,则m的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-11导数的应用一(解析版) 题型:解答题
已知函数f(x)=xlnx-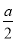 x2.
x2.
(1)当a=1时,函数y=f(x)有几个极值点?
(2)是否存在实数a,使函数f(x)=xlnx-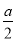 x2有两个极值?若存在,求实数a的取值范围;若不存在,请说明理由.
x2有两个极值?若存在,求实数a的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-10导数的概念及运算(解析版) 题型:填空题
记定义在R上的函数y=f(x)的导函数为f′(x).如果存在x0∈[a,b],使得f(b)-f(a)=f′(x0)(b-a)成立,则称x0为函数f(x)在区间[a,b]上的“中值点”.那么函数f(x)=x3-3x在区间[-2,2]上“中值点”的个数为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-7离散型随机变量及分布列(解析版) 题型:选择题
在15个村庄中有7个村庄交通不便,现从中任意选10个村庄,用ξ表示这10个村庄中交通不便的村庄数,下列概率中等于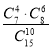 的是( )
的是( )
A.P(ξ=2) B.P(ξ≤2)
C.P(ξ=4) D.P(ξ≤4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com