
【题目】将![]() 个数
个数![]() ,
,![]() ,…,
,…,![]() 的连乘积
的连乘积![]() 记为
记为![]() ,将
,将![]() 个数
个数![]() ,
,![]() ,…,
,…,![]() 的和
的和![]() 记为
记为![]() .(
.(![]() )
)
(1)若数列![]() 满足
满足![]() ,
,![]() ,
,![]() ,设
,设![]() ,
,![]() ,求
,求![]() ;
;
(2)用![]() 表示不超过
表示不超过![]() 的最大整数,例如
的最大整数,例如![]() ,
,![]() ,
,![]() .若数列
.若数列![]() 满足
满足![]() ,
,![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)设定义在正整数集![]() 上的函数
上的函数![]() 满足:当
满足:当![]() (
(![]() )时,
)时,![]() ,问是否存在正整数
,问是否存在正整数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由(已知
的值;若不存在,说明理由(已知![]() ).
).
科目:高中数学 来源: 题型:
【题目】数列1,2,1,2,2,1,2,2,2,1,2,2,2,2,1,2,![]() ,其相邻的两个1被2隔开,第
,其相邻的两个1被2隔开,第![]() 对1之间有
对1之间有![]() 个2,则数列的前209项的和为( )
个2,则数列的前209项的和为( )
A. 279 B. 289 C. 399 D. 409
查看答案和解析>>
科目:高中数学 来源: 题型:
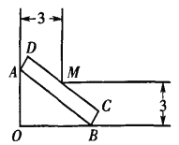
【题目】某建筑物内一个水平直角型过道如图所示.两过道的宽度均为![]() ,有一个水平截面为矩形的设备需要水平移进直角型过道.若该设备水平截面矩形的宽为
,有一个水平截面为矩形的设备需要水平移进直角型过道.若该设备水平截面矩形的宽为![]() ,长为
,长为![]() ,试问:该设备能否水平移进直角型过道?
,试问:该设备能否水平移进直角型过道?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为迎接中华人民共和国成立![]() 周年,开展了以“厉害了,我的国”为主题的征文比赛,评选出一、二、三等奖和优秀奖.校团委根据获奖的结果绘制成了如下两幅不完整的统计图:
周年,开展了以“厉害了,我的国”为主题的征文比赛,评选出一、二、三等奖和优秀奖.校团委根据获奖的结果绘制成了如下两幅不完整的统计图:

(1)扇形统计图中三等奖所在扇形的圆心角的度数是__________度;
(2)请补全条形统计图;
(3)在此次征文比赛中,获得“一等奖”的同学中有两人来自初三年级.现要从获得“一等奖”同学中随机抽选两人参加该校团委组织的征文比赛总结会,请用画树状图或列表法求选中的两人刚好都来自初三年级的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一组数据中的每一个数据都乘以2,再减去80,得到一组新数据,若求得新的数据的平均数是1.2,方差是4.4,则原来数据的平均数和方差分别是( )
A.40.6,1.1B.48.8,4.4C.81.2,44.4D.78.8,75.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C:x2+y2+2kx+(4k+10)y+10k+20=0,其中k≠-1.
(1)求证:曲线C都表示圆,并且这些圆心都在同一条直线上;
(2)证明:曲线C过定点;
(3)若曲线C与x轴相切,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】济南泉城广场上的泉标模仿的是隶书“泉”字,其造型流畅别致,成了济南的标志和象征.李明同学想测量泉标的高度,于是他在广场的A点测得泉标顶端的仰角为60°,他又沿着泉标底部方向前进15.2 m,到达B点,又测得泉标顶部仰角为80°.你能帮助李明同学求出泉标的高度吗?(精确到1 m)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)用篱笆围一个面积为![]() 的矩形菜园,当这个矩形的边长为多少时,所用篱笆最短?最短篱笆的长度是多少?
的矩形菜园,当这个矩形的边长为多少时,所用篱笆最短?最短篱笆的长度是多少?
(2)用一段长为![]() 的篱笆围成一个矩形菜园,当这个矩形的边长为多少时,菜园的面积最大?最大面积是多少?
的篱笆围成一个矩形菜园,当这个矩形的边长为多少时,菜园的面积最大?最大面积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com