练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知抛物线的焦点为，准线为，是上一点，直线与抛物线交于，两点，若，则=

    A.B.

    C.D.

    【答案】B

    【解析】

    先根据题意写出直线的方程，再将直线的方程与抛物线y2＝2x的方程组成方程组，消去y得到关于x的二次方程，最后利用根与系数的关系结合抛物线的定义即可求线段AB的长．

    解：抛物线C：y2＝2x的焦点为F（，0），准线为l：x＝﹣，设M（x1，y1），N（x2，y2），M，N到准线的距离分别为dM，dN，

    由抛物线的定义可知|MF|＝dM＝x1+，|NF|＝dN＝x2+，于是|MN|＝|MF|+|NF|＝x1+x2+1．

    ∵，则，易知：直线MN的斜率为±，

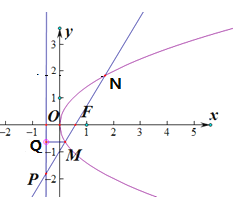
    ∵F（，0），

    ∴直线PF的方程为y＝±（x﹣），

    将y＝±（x﹣），代入方程y2＝2x，得3（x﹣）2＝2x，化简得12x2﹣20x+3＝0，

    ∴x1+x2，于是|MN|＝x1+x2+11

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某大学生在开学季准备销售一种文具盒进行试创业，在一个开学季内，每售出盒该产品获利润元，未售出的产品，每盒亏损元．根据历史资料，得到开学季市场需求量的频率分布直方图，如图所示．该同学为这个开学季购进了盒该产品，以（单位：盒，）表示这个开学季内的市场需求量，（单位：元）表示这个开学季内经销该产品的利润．

    （1）根据直方图估计这个开学季内市场需求量的众数和平均数；

    （2）将表示为的函数；

    （3）根据直方图估计利润不少于元的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某市创卫办为了了解该市开展创卫活动的成效，对市民进行了一次创卫满意程度测试，根据测试成绩评定“合格”、“不合格”两个等级，同时对相应等级进行量化：“合格”计5分，“不合格”计0分，现随机抽取部分市民的回答问卷，统计结果及对应的频率分布直方图如图所示：

    等级

    不合格

    合格

    得分

    频数

    6

    24

    （1）求的值；

    （2）按照分层抽样的方法，从评定等级为“合格”和“不合格”的问卷中随机抽取10份进行问题跟踪调研，现再从这10份问卷中任选4份，记所选4份问卷的量化总分为，求的分布列及数学期望；

    （3）某评估机构以指标（，其中表示的方差）来评估该市创卫活动的成效.若，则认定创卫活动是有效的；否则认为创卫活动无效，应该调整创卫活动方案.在（2）的条件下，判断该市是否应该调整创卫活动方案？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，又有四个零点，则实数的取值范围是（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知在四棱锥中，底面是边长为的正方形，是正三角形，CD平面PAD，E,F,G,O分别是PC,PD,BC,AD 的中点．

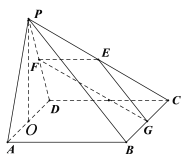
    （Ⅰ）求证：PO平面；

    （Ⅱ）求平面EFG与平面所成锐二面角的大小；

    （Ⅲ）线段上是否存在点，使得直线与平面所成角为，若存在，求线段的长度；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】现有四个函数①y＝x|sinx|，②y＝xcos|x|，③，④y＝xln|x|的部分图象如下,但顺序被打乱,则按照图象从左到右的顺序,对应的函数序号正确的一组是( )

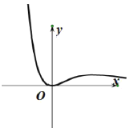
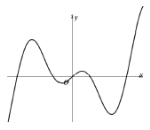
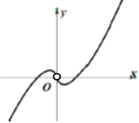
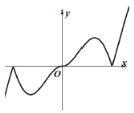
    A.①④②③B.①④③②C.③②④①D.③④②①

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2019年11月份，全国工业生产者出厂价格同比下降，环比下降某企业在了解市场动态之后，决定根据市场动态及时作出相应调整，并结合企业自身的情况作出相应的出厂价格，该企业统计了2019年1~10月份产品的生产数量（单位：万件）以及销售总额（单位：十万元）之间的关系如下表：

    2.08

    2.12

    2.19

    2.28

    2.36

    2.48

    2.59

    2.68

    2.80

    2.87

    4.25

    4.37

    4.40

    4.55

    4.64

    4.75

    4.92

    5.03

    5.14

    5.26

    （1）计算的值；

    （2）计算相关系数，并通过的大小说明与之间的相关程度；

    （3）求与的线性回归方程，并推测当产量为3.2万件时销售额为多少.（该问中运算结果保留两位小数）

    附：回归直线方程中的斜率和截距的最小二乘估计公式分别为，；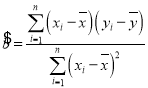

    相关系数.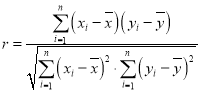

    参考数据：，，.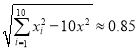

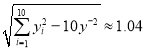    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（为常数，）.

    （Ⅰ）若是函数的一个极值点，求的值；

    （Ⅱ）求证：当时，在上是增函数；

    （Ⅲ）若对任意的（1，2），总存在，使不等式成立，求实数的取范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了提高学生的身体素质，某校高一、高二两个年级共336名学生同时参与了“我运动，我健康，我快乐”的跳绳、踢毽等系列体育健身活动.为了了解学生的运动状况，采用分层抽样的方法从高一、高二两个年级的学生中分别抽取7名和5名学生进行测试.下表是高二年级的5名学生的测试数据（单位：个/分钟）：

    （1）求高一、高二两个年级各有多少人？

    （2）设某学生跳绳个/分钟，踢毽个/分钟.当，且时，称该学生为“运动达人”.

    ①从高二年级的学生中任选一人，试估计该学生为“运动达人”的概率；

    ②从高二年级抽出的上述5名学生中，随机抽取3人，求抽取的3名学生中为“运动达人”的人数的分布列和数学期望.

    查看答案和解析>>

    同步练习册答案