【答案】
分析:(1)利用当n=1时,
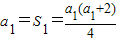
,求a
1的值,根据当n≥2时,a
n=S
n-S
n-1,可求数列{a
n}的通项公式;
(2)证法一、二:先放缩,再裂项求和,即可证得结论;
(3)求出数列{b
n}的通项,证明其单调递增,假设存在这样的实数λ,使得不等式(-1)
n+1λ<b
n对一切n∈N
*都成立,分类讨论求最值,即可求出λ的值.
解答:(1)解:由
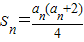
.
当n=1时,
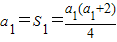
,解得a
1=2或a
1=0(舍去). …2分
当n≥2时,由

∴
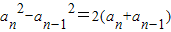
,
∵a
n>0,∴a
n+a
n-1≠0,则a
n-a
n-1=2,
∴{a
n}是首项为2,公差为2的等差数列,故a
n=2n. …4分
(2)证法一:∵

=

,…4分
∴当n≥2时,
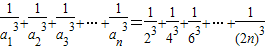

=

.…7分
当n=1时,不等式左边=

显然成立.…8分
证法二:∵n
3-4n(n-1)=n(n
2-4n+4)=n(n-2)
2≥0,∴n
3≥4n(n-1).
∴
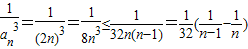
(n≥2).…4分
∴当n≥2时,
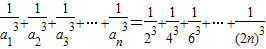

.…7分
当n=1时,不等式左边=

显然成立.…8分
(3)解:由a
n=2n,得
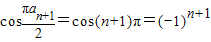
,
设
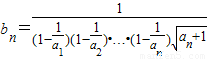
,则不等式等价于.
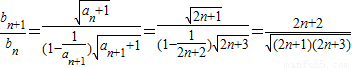
=
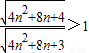
,…9分
∵b
n>0,∴b
n+1>b
n,数列{b
n}单调递增.…10分
假设存在这样的实数λ,使得不等式(-1)
n+1λ<b
n对一切n∈N
*都成立,则
①当n为奇数时,得

; …11分
②当n为偶数时,得
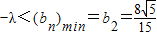
,即

.…12分
综上,

,由λ是非零整数,知存在λ=±1满足条件.…14分
点评:本题考查数列的通项与求和,考查数列与不等式的联系,考查恒成立问题,确定数列的通项,正确放缩,合理运用求和公式是关键.

 (n∈N*).
(n∈N*). +
+ +
+ +…+
+…+ <
<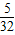 (n∈N*);
(n∈N*); )(1-
)(1- )…(1-
)…(1- )cos
)cos <
< 对一切n∈N*都成立?若存在,求出λ的值;若不存在,说明理由.
对一切n∈N*都成立?若存在,求出λ的值;若不存在,说明理由.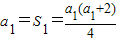 ,求a1的值,根据当n≥2时,an=Sn-Sn-1,可求数列{an}的通项公式;
,求a1的值,根据当n≥2时,an=Sn-Sn-1,可求数列{an}的通项公式;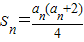 .
.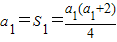 ,解得a1=2或a1=0(舍去). …2分
,解得a1=2或a1=0(舍去). …2分
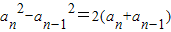 ,
, =
= ,…4分
,…4分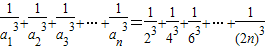
 =
= .…7分
.…7分 显然成立.…8分
显然成立.…8分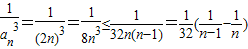 (n≥2).…4分
(n≥2).…4分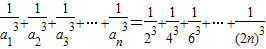
 .…7分
.…7分 显然成立.…8分
显然成立.…8分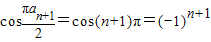 ,
,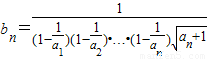 ,则不等式等价于.
,则不等式等价于.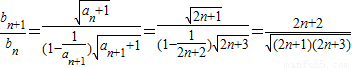 =
=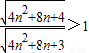 ,…9分
,…9分 ; …11分
; …11分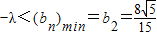 ,即
,即 .…12分
.…12分 ,由λ是非零整数,知存在λ=±1满足条件.…14分
,由λ是非零整数,知存在λ=±1满足条件.…14分

 阅读快车系列答案
阅读快车系列答案