
分析 (1)当直线过原点时,直接写出直线方程,当不过原点时,设出直线的截距式方程x+y=a,代入点的坐标求解a,则答案可求.
(2)求出直线AB的斜率,线段AB的垂直平分线l方程,然后求解圆心C的坐标,圆的半径,然后求解圆的方程.
解答 解:(1)解:当直线过原点时,直线方程为y=$\frac{4}{3}$x,即4x-3y=0;
当直线不过原点时,设直线方程为x+y=a.
则3+4=a,得a=7.
∴直线方程为x+y-7=0.
∴过点M(3,4)且在坐标轴上截距相等的直线方程为4x-3y=0或x+y-7=0.
故答案为:4x-3y=0或x+y-7=0.
(2)因为A(1,1),B(2,-2),所以线段AB的中点D的坐标为$({\frac{3}{2},-\frac{1}{2}})$,直线AB的斜率为${k_{AB}}=\frac{-2-1}{2-1}=-3$,因此线段AB的垂直平分线l方程为$y+\frac{1}{2}=\frac{1}{3}({x-\frac{3}{2}})$,即x-3y-3=0
圆心C的坐标是方程组$\left\{{\begin{array}{l}{x-3y-3=0}\\{x-y+1=0}\end{array}}\right.$的解,解此方程组得$\left\{{\begin{array}{l}{x=-3}\\{y=-2}\end{array}}\right.$,
所以圆心C的坐标为(-3,-2)圆的半径$r=|{AC}|=\sqrt{{{({1+3})}^2}+{{({1+2})}^2}}=5$,
所以圆的方程为(x+3)2+(y+2)2=25.
点评 本题考查了直线的点斜式方程和截距式方程,考查了分类讨论的数学思想方法,圆的方程的求法,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:选择题
| A. | 由圆x2+y2=r2的面积S=πr2,猜想椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的面积S=πab | |
| B. | 由金、银、铜、铁可导电,猜想:金属都可导电 | |
| C. | 猜想数列$\frac{1}{1•2}$,$\frac{1}{2•3}$,$\frac{1}{3•4}$的通项公式为an=$\frac{1}{n(n+1)}$(n∈N*) | |
| D. | 半径为r的圆的面积S=πr2,则单位圆的面积S=π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2>b2 | B. | $\frac{1}{a}<\frac{1}{b}$ | C. | ac2>bc2 | D. | $\frac{a}{{{c^2}+1}}>\frac{b}{{{c^2}+1}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届宁夏高三上月考一数学(理)试卷(解析版) 题型:解答题
已知函数 (
(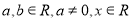 ).
).
(1)若函数 的图象过点
的图象过点 ,函数
,函数 有且只有一个零点,求
有且只有一个零点,求 表达式;
表达式;
(2)在(1)的条件下,当 时,
时, 是单调函数,求实数
是单调函数,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com